使用 Spyder 进行金融数据分析#
通过本工作坊，参与者将能够有效地使用 Spyder，应用一些规范的金融理论和模型来构建资产组合，从而在给定风险水平下实现预期收益最大化。通过这种方式，将使用基于统计的工具来构建投资组合。
先决条件#
为了跟进本工作坊，我们建议您具备中级 Python 知识。您可以访问 Python 教程来学习该编程语言的基础知识或巩固您的 Python 知识。
您还需要安装 Anaconda（或 Miniconda）和 Spyder。有关 Spyder 安装的更多信息请参阅安装指南。
重要
Spyder 现在提供适用于 Windows 和 macOS 的独立安装程序，让您无需下载 Anaconda 或在现有环境中手动安装即可更轻松地启动和运行应用程序。虽然我们仍然支持 Anaconda，但我们建议在这些平台上使用此安装方法，以避免大多数软件包冲突和其他问题。
此外，最好具备以下先验知识
中级 Python 水平
统计学基础知识
最好具备一些金融计量经济学知识
学习目标#
完成本工作坊后，您应该能够：
对股票和加密货币投资组合应用初级统计分析，以衡量其表现
了解使用 IDE 编程的优势，例如使用变量查看器检查变量以及利用绘图窗格与绘图交互。
学习者画像#
本工作坊适用于对金融感兴趣并希望使用 Python 和 Spyder 迈出金融分析第一步的人。
简介#
在本工作坊中，我们将从 Yahoo! Finance API 实时获取金融数据，并使用计量经济学和计算工具探索金融投资组合。
为什么使用 Python 进行金融分析？#
对历史和当前金融数据进行实时分析对于金融工具投资者至关重要。Python 具有许多使其成为金融任务理想选择的特性：
无论是否有编程经验，任何人都易于学习
它可以连接到 API 以实时加载金融数据
它是机器学习（监督学习、无监督学习、强化学习）资源最丰富的编程语言，而机器学习是当今计量经济学最有用的工具之一
它有优秀的绘图库
您可以使用 Google Colab 或 Binder 等资源在云端进行分析。
我为什么要使用 IDE？#
尽管您可以在没有 IDE（集成开发环境）的情况下使用 Python，但使用 IDE 会大大提高工作效率。Spyder 是一个用 Python 编写的科学集成开发环境，由科学家、工程师和数据分析师设计，也为他们服务。Spyder 的功能及其与 Python 的集成使其非常适合金融分析。
Spyder 金融分析入门#
如果您不熟悉 Spyder，我们建议您从我们的快速入门开始。但如果您想了解摘要，这里有一个快速概览。
注意
如果您已经有使用 Spyder 的经验，可以跳过本节。
编辑器#
编辑器是您编写代码并将其保存为文件（脚本）的地方。它允许您轻松地保留您的工作。您可以在此处编写您想从 IPython 控制台中进行的数据分析中保留的代码。您还可以在此处读取、编辑和运行本工作坊的代码。
IPython 控制台#
IPython 控制台是 Spyder 的组件，您可以在其中编写要试验的代码块。在本工作坊中，我们将为您提供可以在此控制台中复制和运行的代码片段。
本质上，IPython 控制台允许您使用 Python 执行命令并与数据交互。
变量探索器#
变量查看器是 Spyder 最好的功能之一。它允许您交互式地浏览和管理当前选定的IPython 控制台会话中代码生成的对象。
变量查看器是本工作坊中最常用的组件之一。这是我们将观察数据和大部分分析结果（绘图除外）的窗格。
绘图窗格#
绘图窗格显示了 IPython 控制台会话中创建的所有静态图表和图像。所有由代码生成的绘图都将出现在此组件中。此窗格还允许您将每个图形保存到本地文件或复制到剪贴板以与他人共享。
准备工作#
在开始之前，您必须安装运行代码所需的一些软件包和库。我们建议您在虚拟环境中安装这些依赖项。我们在这里逐步解释如何操作。
设置 Conda 环境#
如果您想将 Spyder 放在一个专用环境中，以便与您的其他软件包分开更新并避免任何冲突，您可以这样做。
您可以通过两种不同的方式设置您的环境。
重要
我们建议使用 Anaconda（或 Miniconda）创建虚拟环境，因为它与 Spyder 无缝集成。您可以在 Anaconda 文档中找到安装说明。
使用命令#
只需在 Anaconda Prompt（Windows）或终端（其他平台）中运行以下命令，即可创建一个名为 financial-analysis 的新环境。
$ conda create -n financial-analysis
要同时安装 Spyder 的可选依赖项以获得完整功能，请使用以下命令
$ conda activate financial-analysis
$ conda install -c conda-forge numpy scipy pandas matplotlib sympy cython spyder-kernels requests multitasking lxml tqdm
$ pip install -i https://pypi.anaconda.org/ranaroussi/simple yfinance
$ pip install Historic-Crypto
重要
Spyder 现在提供适用于 Windows 和 macOS 的独立安装程序，让您无需下载 Anaconda 或在现有环境中手动安装即可更轻松地启动和运行应用程序。
下载数据集#
虽然在工作坊期间我们将解释如何使用一些 API 下载最新数据，但您也可以从此链接下载 csv 格式的数据集。
要完成本工作坊，您无需创建新目录。但是，如果您下载了数据并想使用它而不是 API，则必须将包含下载数据的目录设置为工作目录。为此，请检查工作目录是否正确。您应该在右上角看到下载数据所在目录的路径。如下所示：
在 Spyder 中设置虚拟环境#
让我们检查一下我们创建的虚拟环境是否在 Spyder 中启用。转到 偏好设置 > Python 解释器，然后使用 使用以下 Python 解释器 下拉菜单选择您的虚拟环境。您应该会看到如下内容：
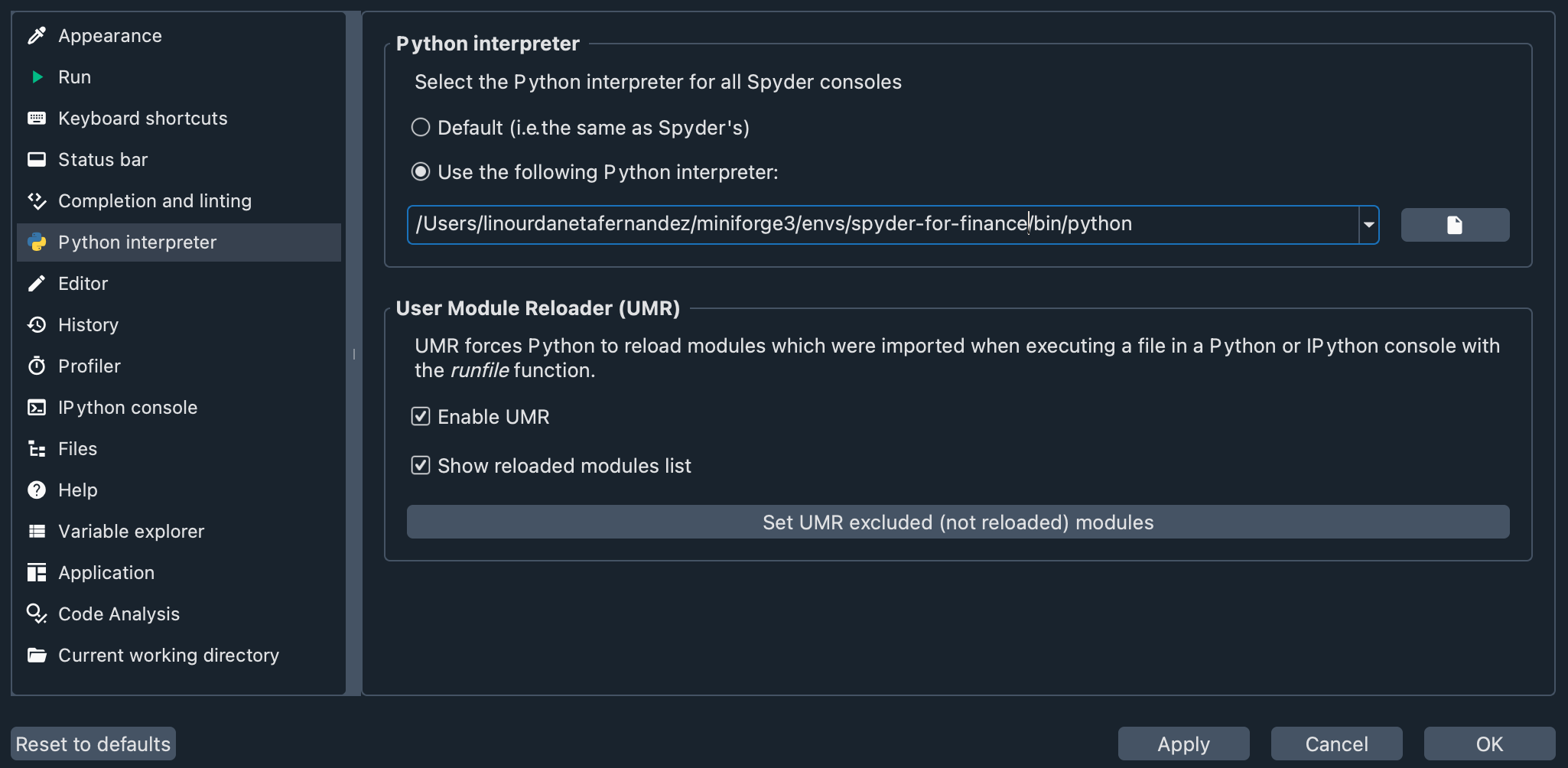
现在，您已准备好继续进行工作坊。
下载代码#
尽管本工作坊旨在让您在 IPython 控制台中编写代码，但我们创建了一个您可以从此处下载的文件。此脚本提供了您将在本工作坊中编写的所有代码，如果您迷路了，可以将其用作指南。
获取金融数据#
在金融领域，保持最新信息非常重要。因此，我们将使用一个 Python 库，它允许我们从 Yahoo! Finance API 获取最新的历史股票市场记录。通过这种方式，我们将能够下载我们感兴趣的分析期间的数据。
请记住，本工作坊的所有代码都应在 Spyder 右下角的“IPython 控制台”中输入并运行。
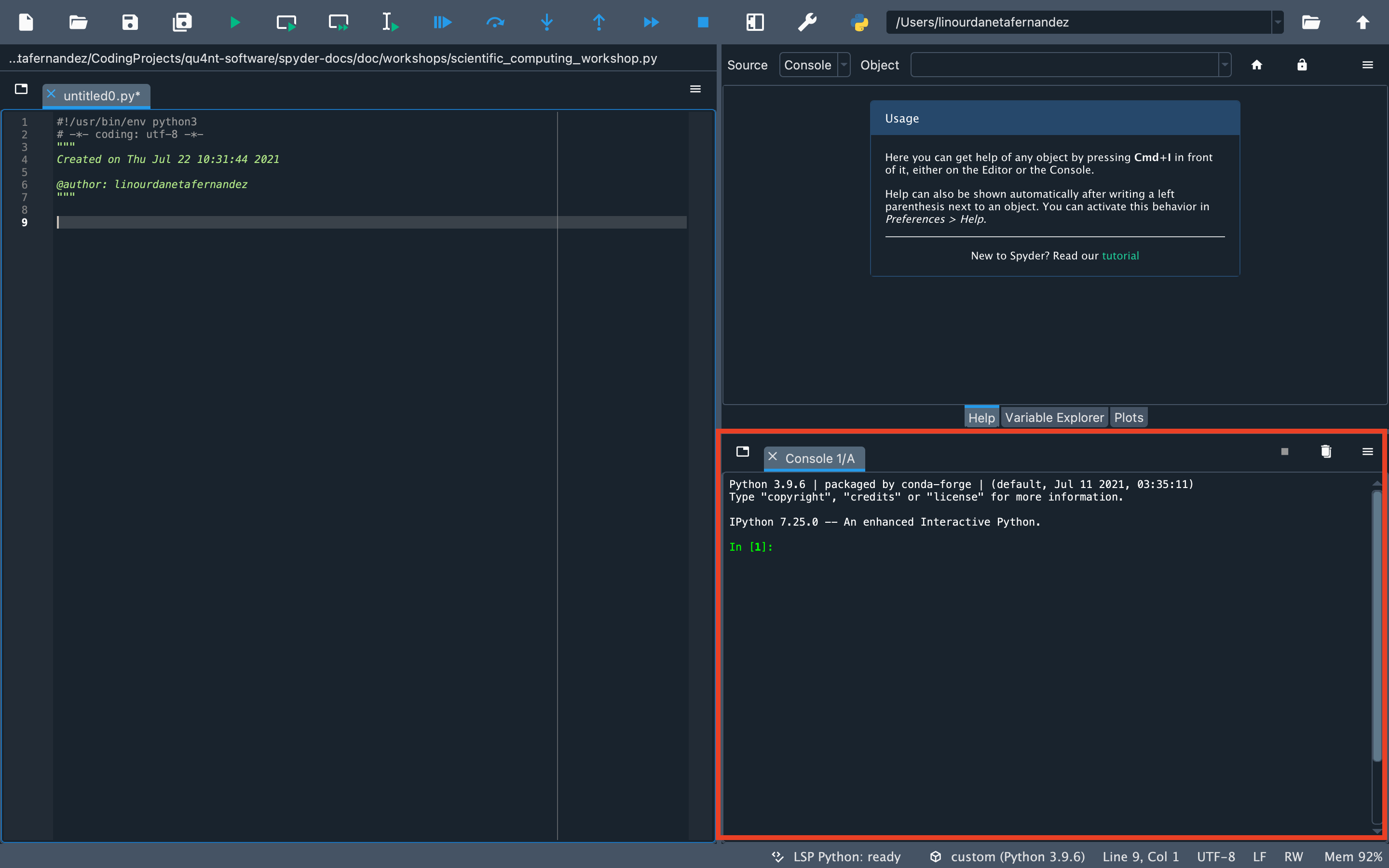
您也可以在编辑器（占据 Spyder 整个左侧的窗格）中编写代码。如果您使用编辑器，可以通过选择代码并点击运行工具栏中的运行选定或当前行按钮，或者按 F9 键来运行代码。
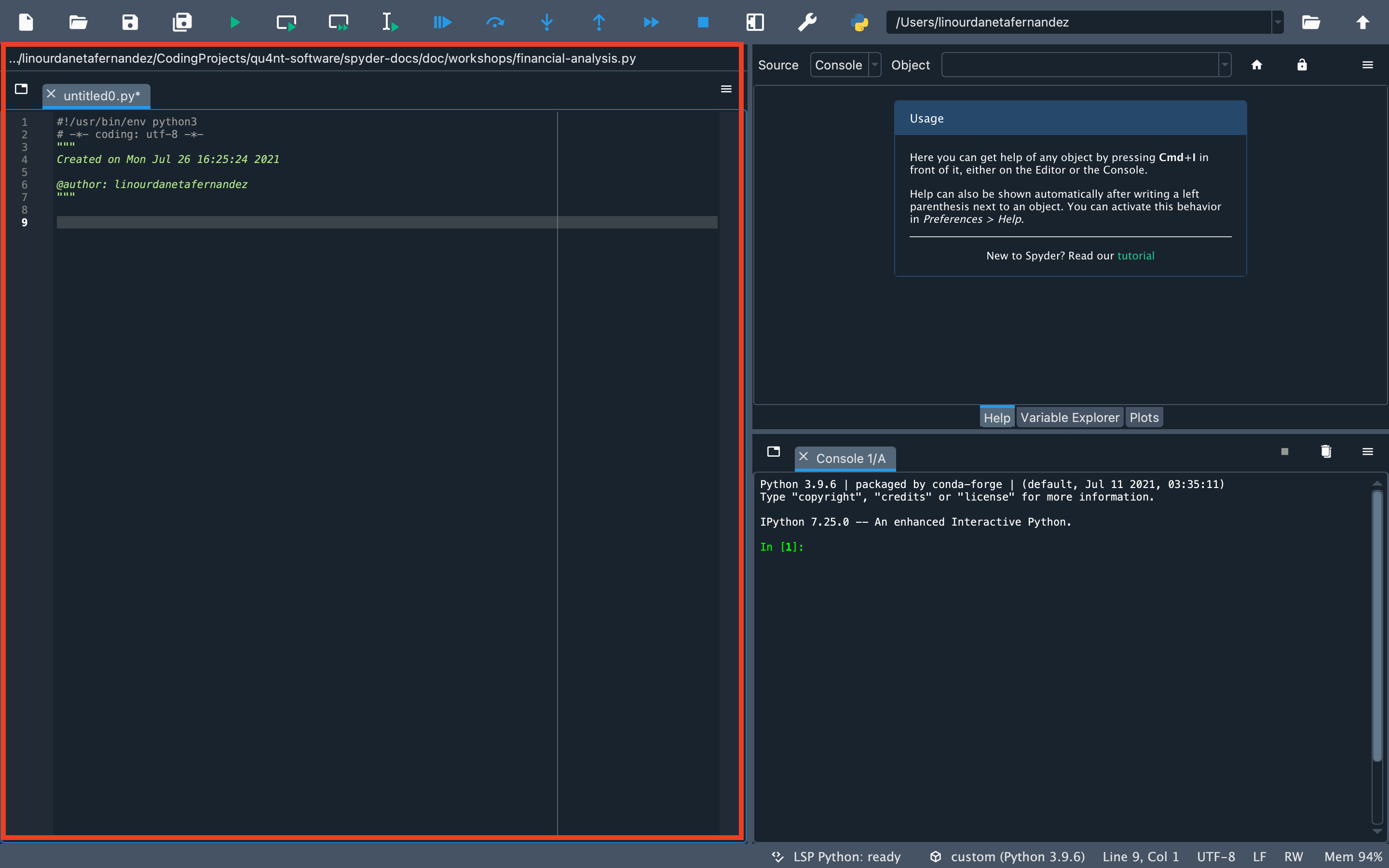
首先，导入库。
import numpy as np
import pandas as pd
import matplotlib as mpl
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import pprint
from Historic_Crypto import Cryptocurrencies
from Historic_Crypto import HistoricalData
import yfinance as yf
第一组导入用于基本操作。第二组（Historic_Crypto 和 yfinance）导入我们将用于下载金融数据的库。
让我们以一个例子开始探索库。我们将用一行代码获取 Netflix 的金融信息
netflix = yf.Ticker("NFLX")
我们使用了 yfinance 库的 Ticker 类来创建一个 netflix 对象。此对象包含我们可以查询的属性和方法，以获取各种类型的信息。
一般股票信息#
如果您想知道可以查询哪些方法和属性，可以使用内置的 help() 函数。
您也可以在控制台中输入对象名称（netflix），然后输入一个句点并按一次 Tab 键。IPython 的建议将出现，以帮助您浏览对象。
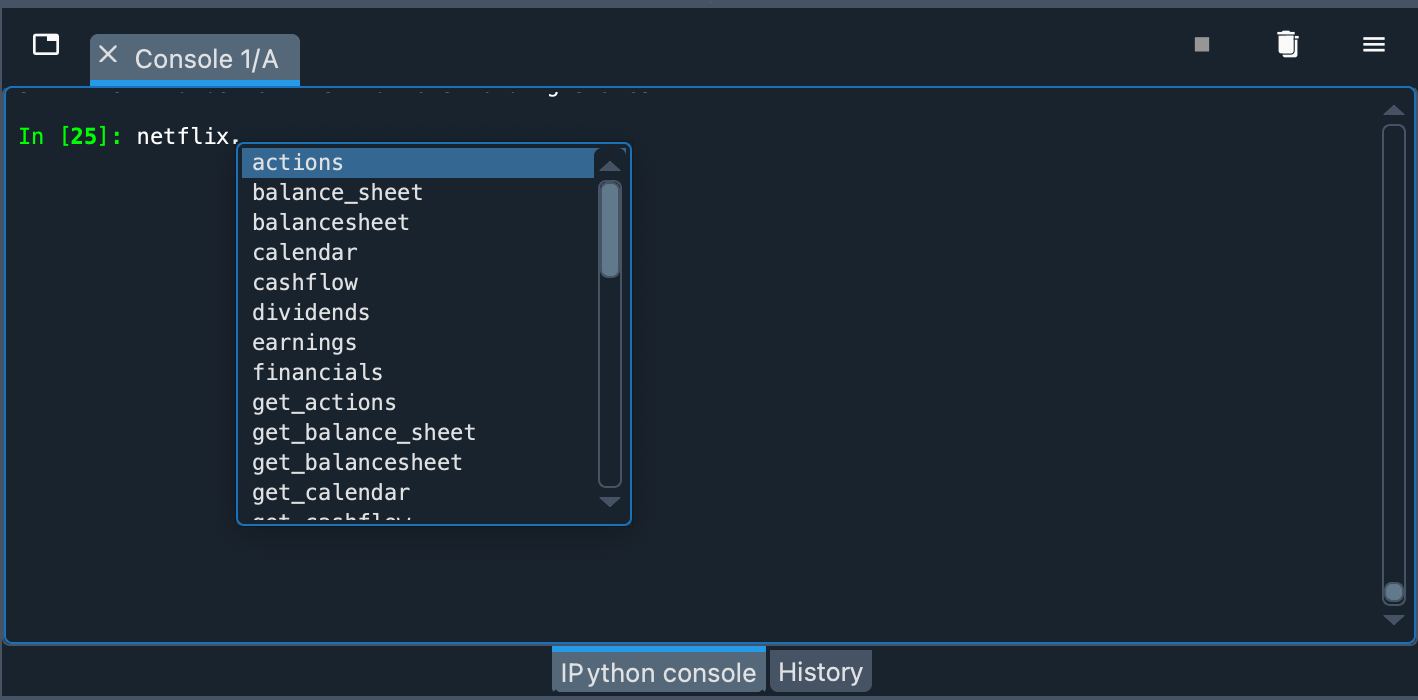
例如，我们可以使用对象的 info 属性获取一般信息。
netflix_info = netflix.info
我们可以在变量查看器中，在 netflix_info 变量中观察结果。
如果双击它，将显示一个包含详细信息的新窗口。
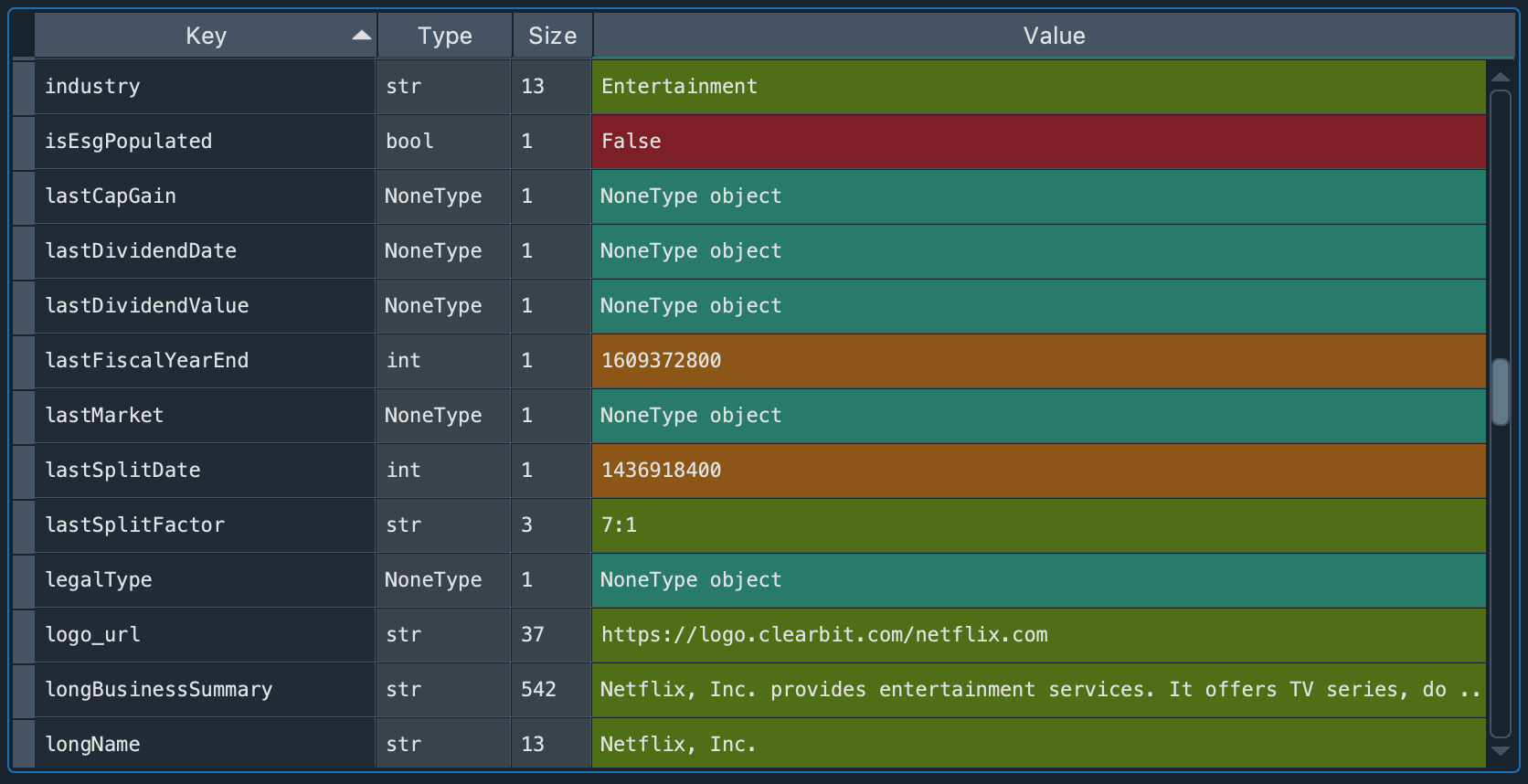
在该窗口中，我们可以看到一个 Python 字典，其中每个键都分配了一个值。每种类型的值都以独特的颜色表示。例如，我们看到 Netflix 是娱乐行业，业务类型的摘要，以及其他指标。变量查看器是查看这些类型结果的一种非常便捷的方式。我们可以将其与在 IPython 控制台中使用 pprint 函数查看进行比较
pprint.pprint(netflix_info)
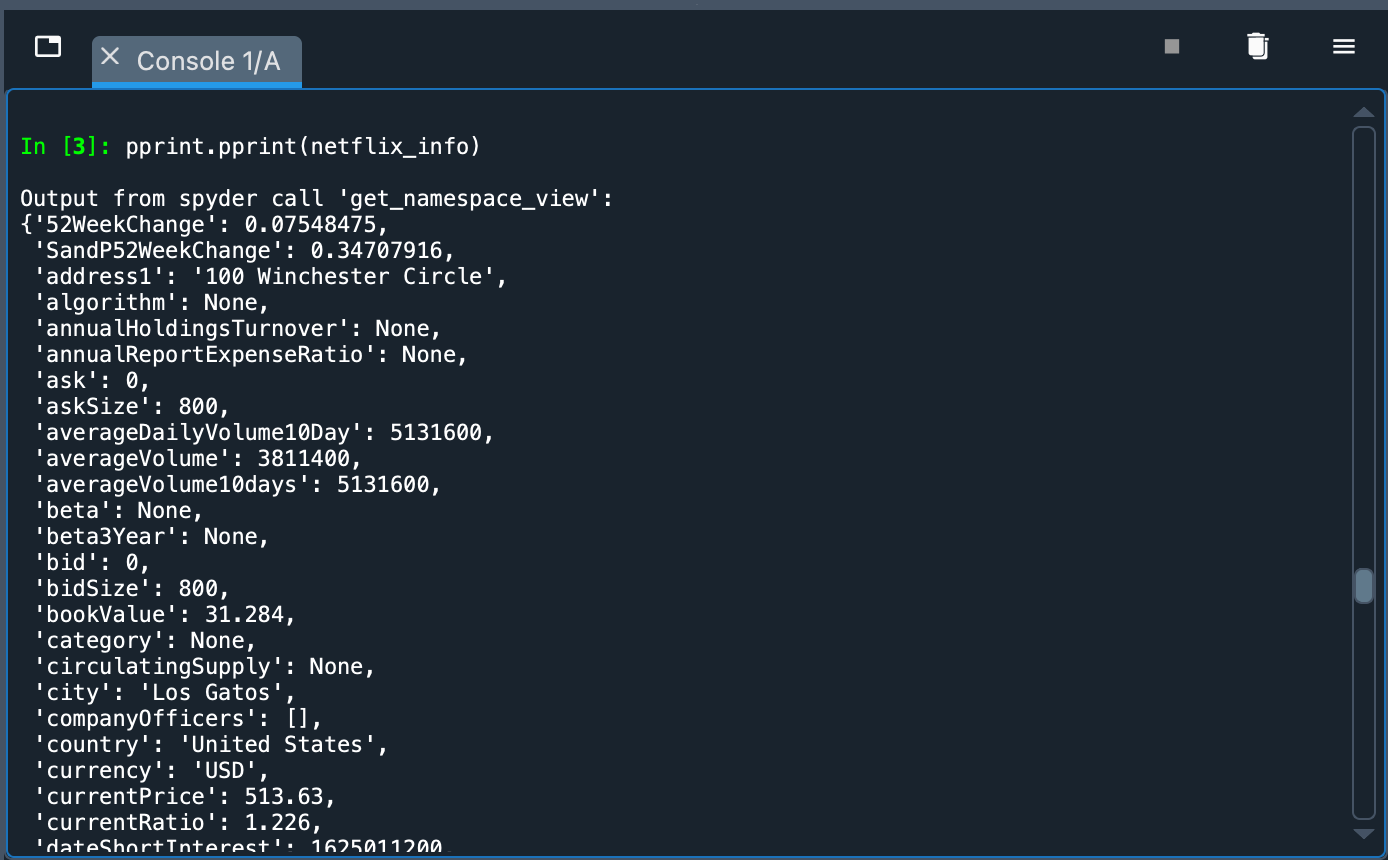
尽管 pprint 显示所有信息，但在变量查看器中查看更容易。
历史股票数据#
我们可以使用以下代码行在数据集中下载股票的历史记录
hist = netflix.history(period="max")
我们可以在变量查看器中看到此数据集的摘要和更多详细信息。它显示为一个 DataFrame 对象，有 7 列和数千行。如果双击它，我们将看到按日期升序排列的 Netflix 股票历史记录。
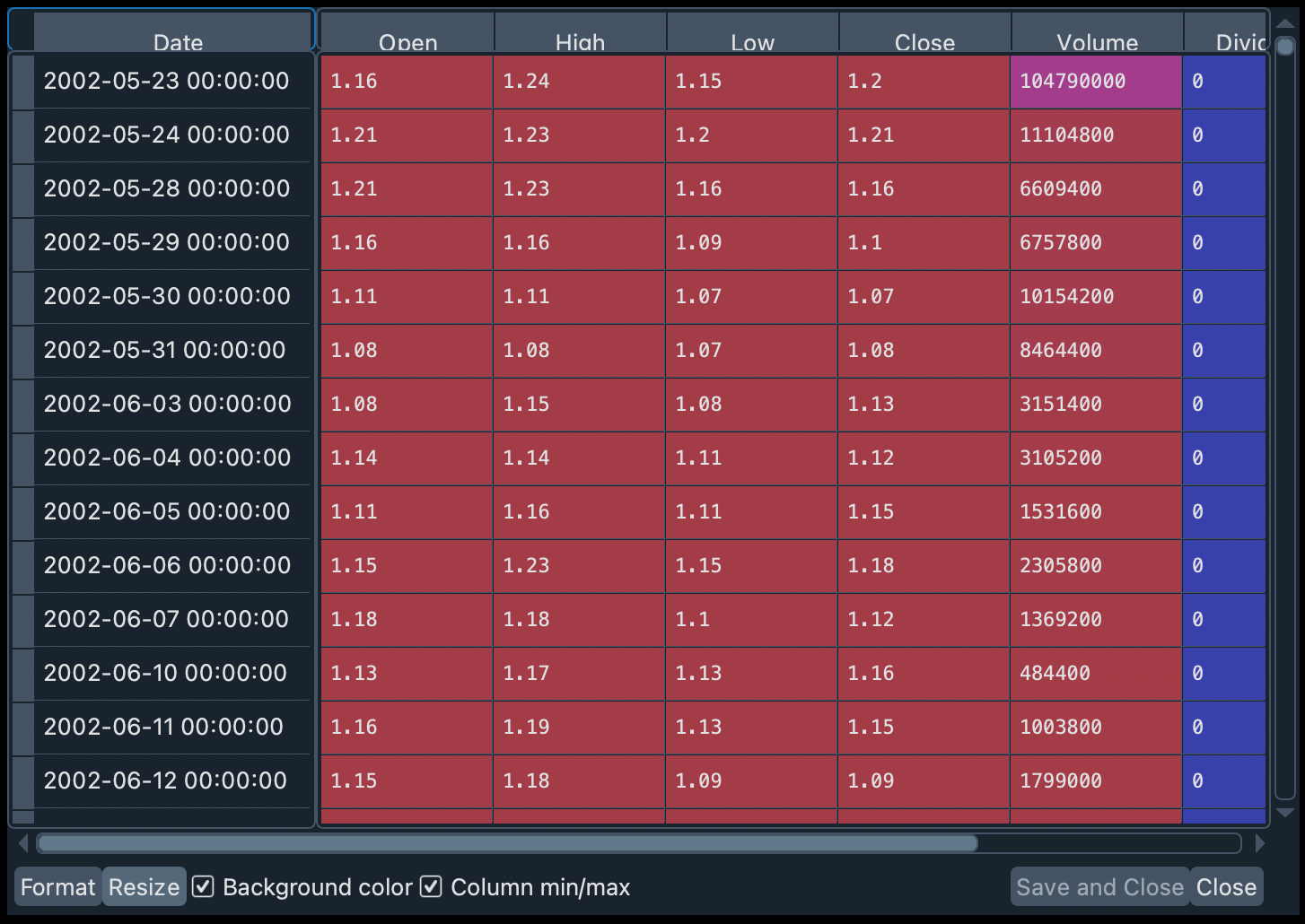
在整个工作坊中，我们将使用这些历史信息，通过各种规范的金融理论来比较不同类型的金融投资组合。
第一个投资组合#
让我们构建我们的第一个股票投资组合！假设我们对投资科技感兴趣，并且我们想知道将资金投入该行业的一些“巨头”可以获得什么样的回报。
为了衡量我们第一个投资组合的表现，我们将使用金融界的一个经典理论：均值-方差投资组合 (MVP) 理论。该模型假设投资者只关心预期收益和这些收益的方差。分析完全基于股票价格时间序列的统计度量，例如周期性平均收益和相同周期性收益的方差。
准备投资组合数据#
在我们开始之前，让我们运行一些代码行来设置绘图样式。这些行是可选的，但我们建议您运行它们，以便图形看起来像我们在本工作坊中提供的屏幕截图。
plt.style.use("fivethirtyeight")
mpl.rcParams["savefig.dpi"] = 300
mpl.rcParams["font.family"] = "serif"
np.set_printoptions(precision=5, suppress=True, formatter={"float": lambda x: f"{x:6.3f}"})
假设我们想衡量由谷歌、苹果、微软、Netflix 和亚马逊股票组成的投资组合的表现。我们称这个集合为 SYMBOLS_1。
SYMBOLS_1 = ["GOOG", "AAPL", "MSFT", "NFLX", "AMZN"]
注意
如果您在变量查看器中搜索 SYMBOLS_1，您会找不到它：Python 将此元素解释为常量，而不是变量。这是因为名称是用大写字母书写的（没有小写字母）。默认情况下，变量查看器不显示这一点，但实际上您可以在偏好设置中更改设置，以便能够看到这些常量。
我们将下载此投资组合的历史数据。为此，我们将使用 yfinance 的 download() 函数，该函数以一个包含上面定义的符号（SYMBOLS_1）的字符串作为第一个参数。其余参数是开始日期（start="2012-01-01"）、结束日期（end="2021-01-01"）以及数据如何分组（group_by="Ticker"）。
data_1 = yf.download(" ".join(SYMBOLS_1), start="2012-01-01", end="2021-01-01", group_by="Ticker")
最后一个参数（group_by="Ticker"）主要按股票对信息进行分组。否则，主要分组是按交易信息类型（例如，开盘价、收盘价、交易量）进行。在下图中，您可以看到差异（上方是默认组织，下方是按“股票代码”分组）。
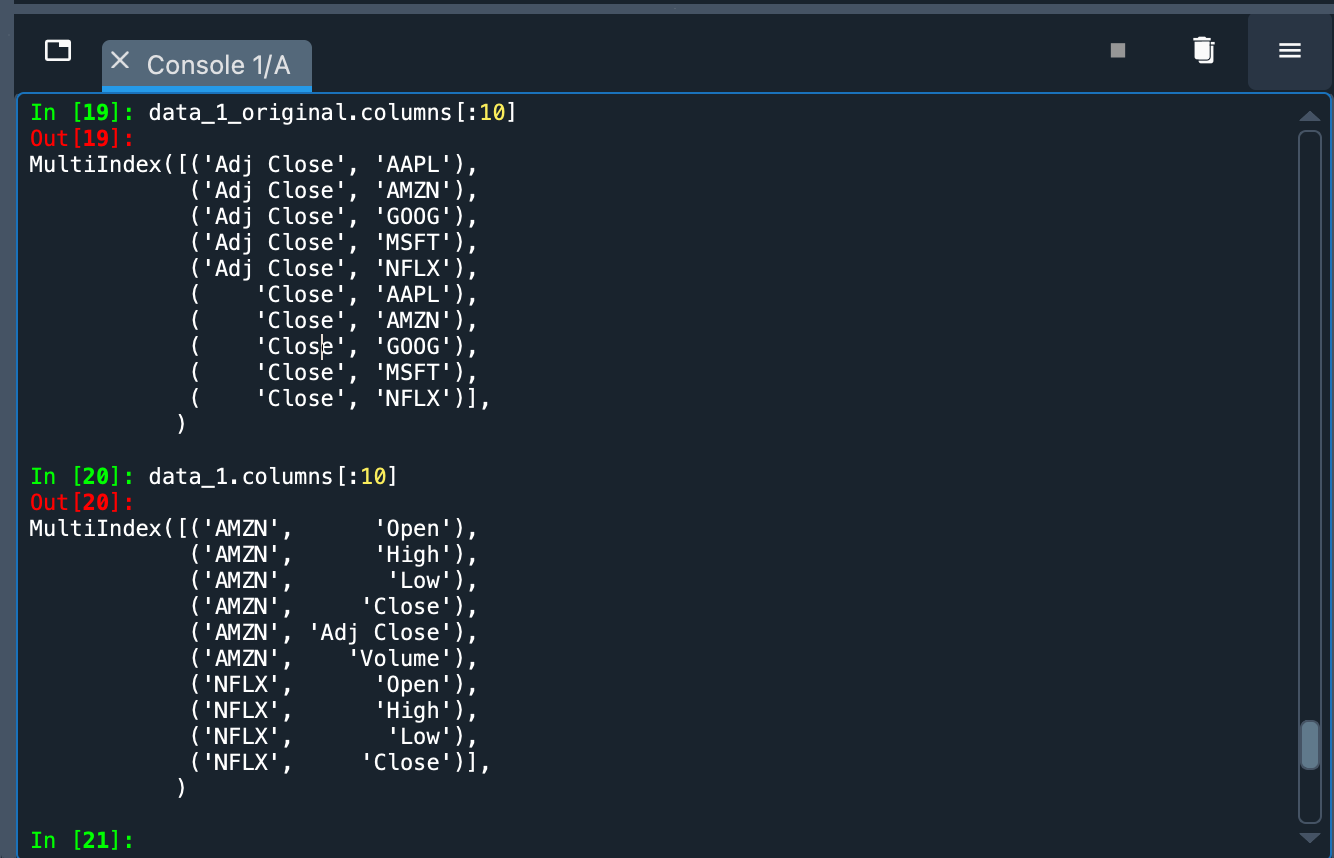
历史数据已作为 Pandas DataFrame 下载。我们可以在变量查看器中的变量 data_1 中探索这些数据。
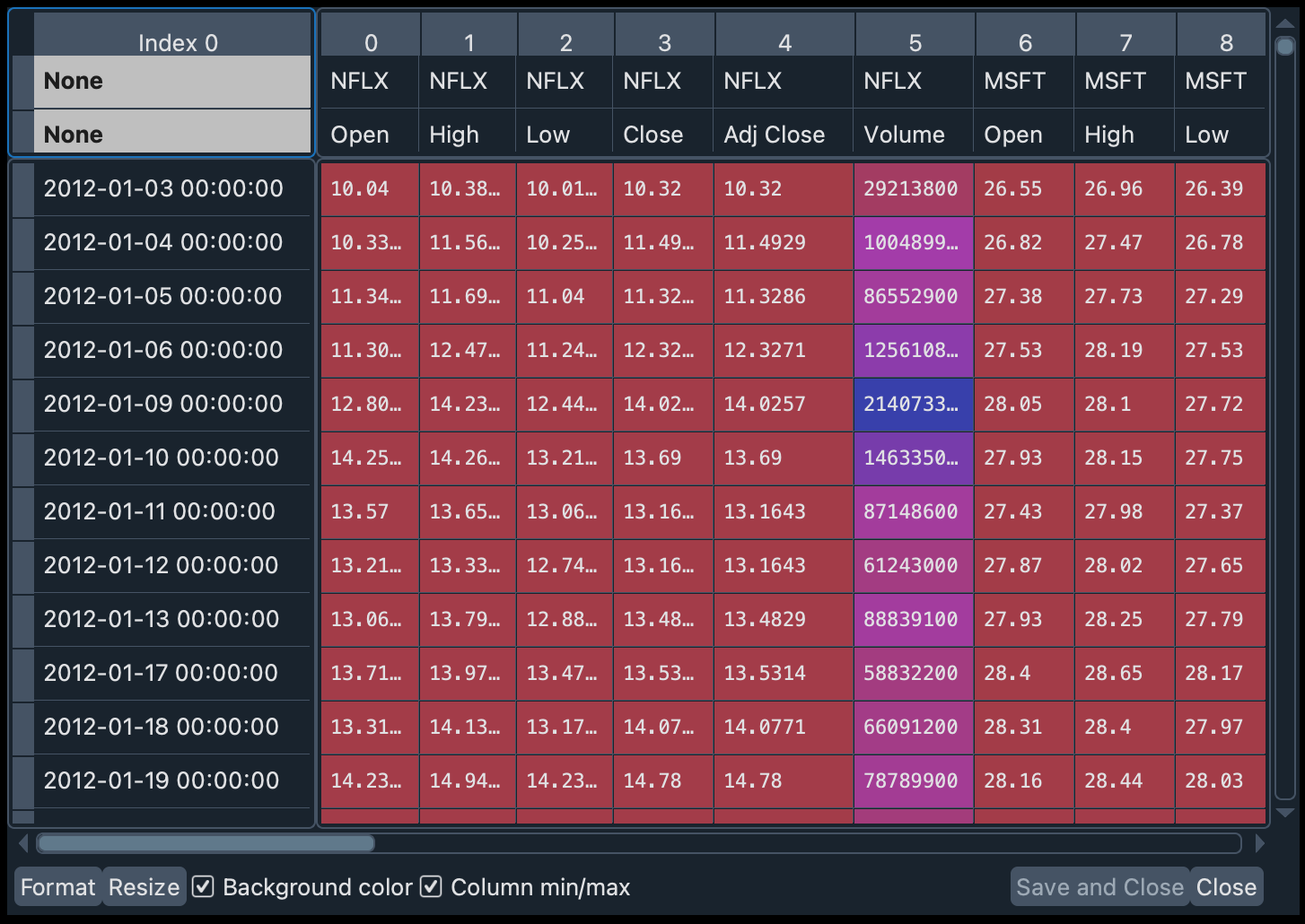
让我们稍微改变一下数据的格式，使符号显示为列名，并将股票代码从列移动到行。我们将使用 DataFrame 的 stack() 操作来完成此操作。
data_1 = data_1.stack(level=1).rename_axis(["Date", "Ticker"]).reset_index(level=1)
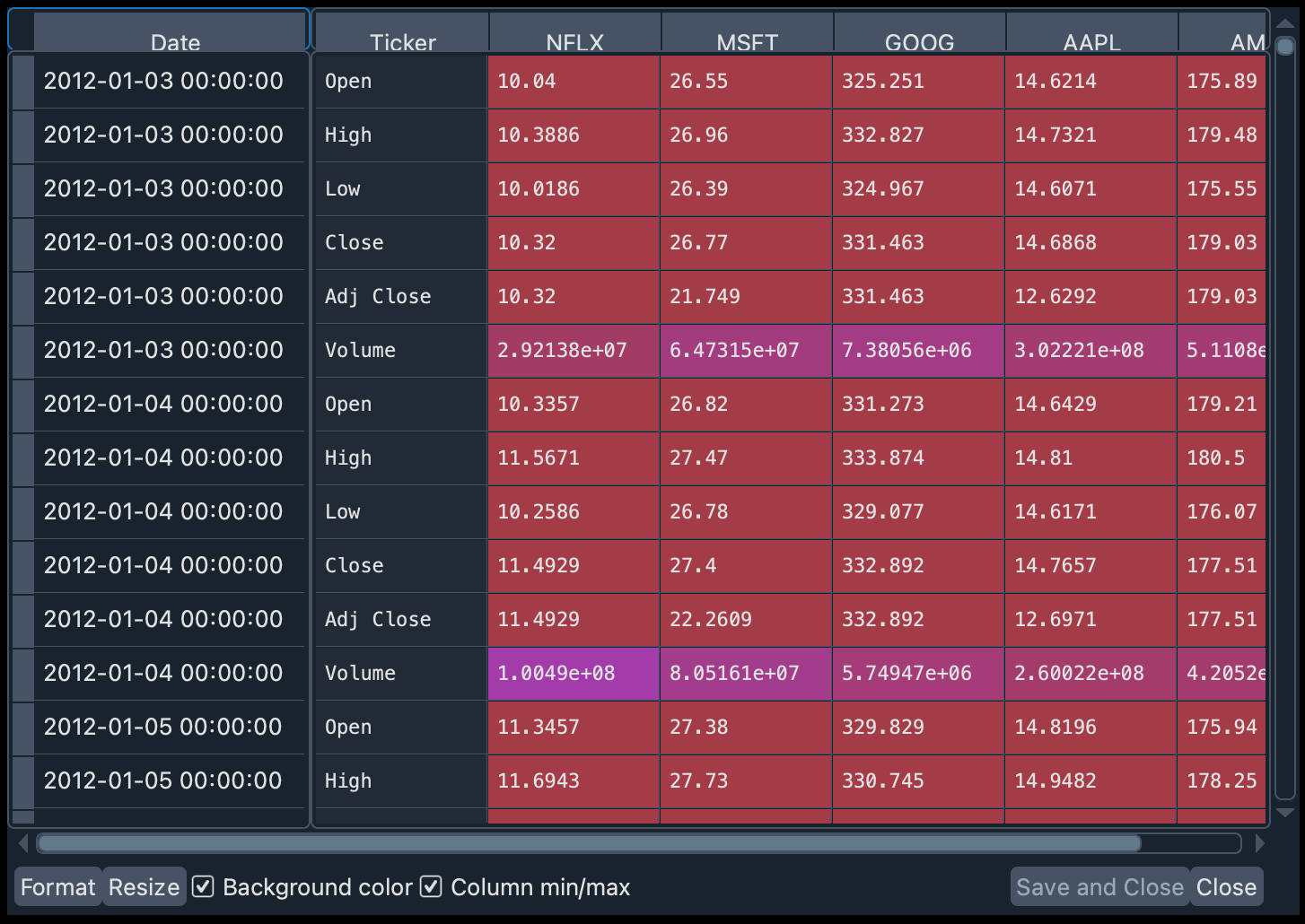
从股票代码中，我们只对每日收盘价感兴趣。所以我们只保留 "Close" 的值，然后删除股票代码列。
close_data_1 = data_1[data_1.Ticker == "Close"].drop("Ticker", inplace=False, axis=1)
您会注意到变量查看器中有一个新的 DataFrame，名为 close_data_1，包含 2,265 行和 5 列。
投资组合概览#
我们想看看如果我们从 2012 年到 2021 年初投资于我们的投资组合，它的表现会如何。我们如何获得这个衡量标准呢？让我们看看每只股票的月度收盘价。为此，我们将对数据进行自动重采样。然后我们将计算相对频率（百分比）的变化。
重采样将使用 resample("M") 方法执行，百分比计算将使用 pct_change() 方法执行。结果将存储在 monthly_data_1 变量中。
monthly_data_1 = close_data_1.resample("M").ffill().pct_change()
由于每只股票都是一列，我们可以对 DataFrame 使用 mean() 方法来查看结果。
monthly_data_1.mean()
# AMZN 0.029931
# GOOG 0.018784
# MSFT 0.020698
# AAPL 0.023033
# NFLX 0.042060
# dtype: float64
重要
请记住，此收盘信息表示每只股票的相对增长，而不是其以任何货币计价的收盘价。
正如我们所看到的，所有结果都是正的，所以这个投资组合在这些年里一直盈利。相对而言，最大的收益将来自 Netflix（0.4%）。这些百分比显示了股票价格月度变化的平均值。但是这些价格有多稳定呢？为了找出答案，我们可以计算股票价格增长的标准差。
monthly_data_1.std()
# AMZN 0.082308
# GOOG 0.061057
# MSFT 0.058395
# AAPL 0.081239
# NFLX 0.145416
# dtype: float64
Netflix 的波动性最高（0.1454），这表明其价格尽管增长最快，但在这些年里也经历了很多变化。另一方面，微软的价格最稳定（0.0583）。
观察增长和可变性的一个好方法是绘制时间序列图。为了缩放值，我们将把股票收盘价的相对频率除以它在数据框 close_data_1 中的初始值（这些初始值可以通过 close_data_1.iloc[0]) 找到）。该图使用 Pandas DataFrame 的 plot() 方法绘制（我们向其传递图的大小和图标题作为参数）。
(close_data_1/close_data_1.iloc[0]).plot(figsize=(16, 10), title="Portfolio 1 daily stock price")
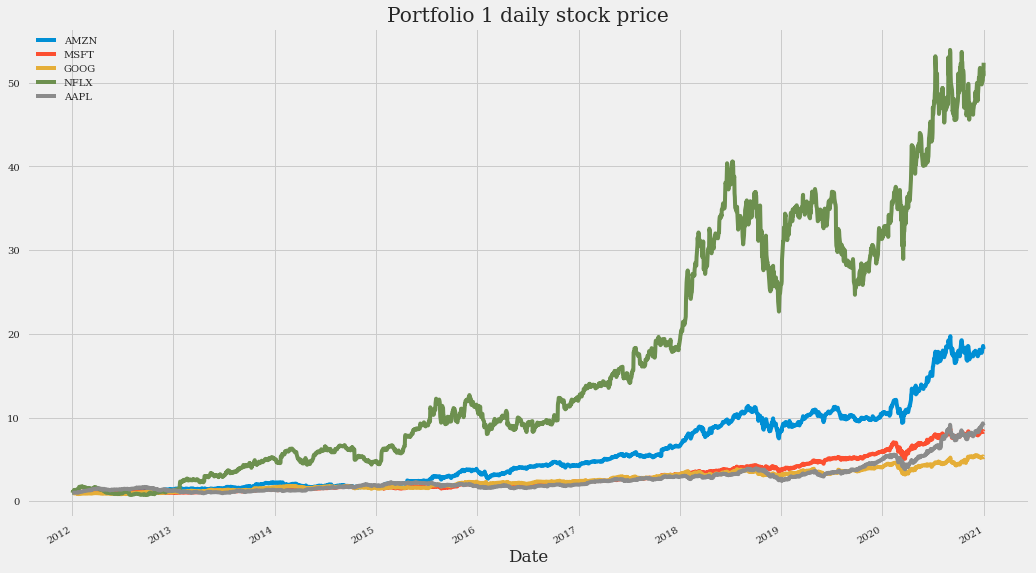
重要
您将能够在绘图窗格中看到图表。在左侧，您将看到详细的绘图。在右侧，将创建一个堆栈，其中包含在控制台中以及直接在编辑器中运行代码生成的所有绘图。您可以通过右键单击或触控板来复制、删除或将绘图保存到磁盘。
上述时间序列图清楚地显示了所有股票的增长，尤其是 Netflix。上面讨论的高波动性也可以看出。例如，从图表中可以看出，由于高波动性，在 2014 年和 2019 年投资 Netflix 几乎没有留下任何利润（如果年初购买股票并在年末立即出售）。
我们也可以使用 plot() 方法绘制我们已有的月度数据 DataFrame。为此，我们将所有值加 1 并使用 cumprod() 方法计算累积乘积。
(monthly_data_1 + 1).cumprod().plot(figsize=(16, 10), title="Portfolio 1 monthly stock price")
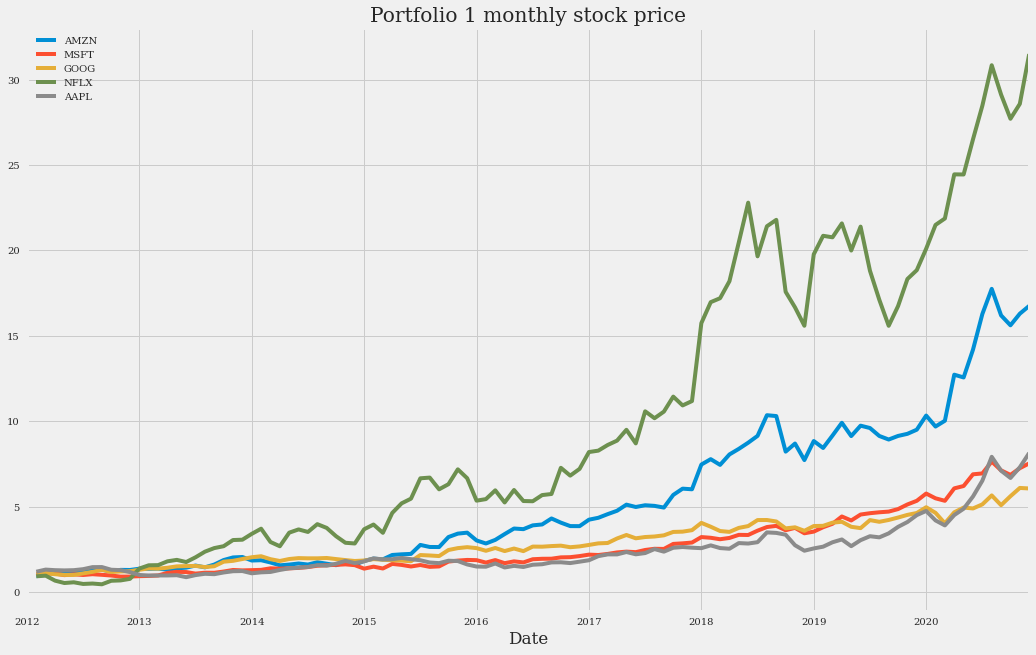
这个月度数据图比每日数据图“更平滑”。
收益和波动率#
请记住，在均值-方差投资组合理论中，重要的是预期收益和方差。为了计算这些收益，我们将一只股票某一天的价格除以同一只股票前一天的价格。我们将通过将 close_data_1 DataFrame 除以其自身的一个版本来完成此操作，该版本中我们将每个记录向后移动一个日期（shift(1)）。例如，如果 2012-01-03 日某只股票价值 1，而第二天（2012-01-02）价值 2，那么在我们的移位数据集中，2012-01-03 日该股票将价值 1。通过这种方式，我们将 1 除以 2。所有股票的所有值都以此类推。我们还将通过使用 np.log() 将结果转换为对数刻度来对其进行归一化。
注意
趋势线在对数刻度下更容易绘制，因为它们更倾向于与最小值拟合。此外，对数刻度提供了更真实的股价走势视图。
rets_1 = np.log(close_data_1/close_data_1.shift(1)).dropna()
在变量 rets_1 中，您可以看到结果 DataFrame。如果您双击变量查看器中的变量名，您会看到有正值（股价上涨）和负值（收盘时股价下跌）。
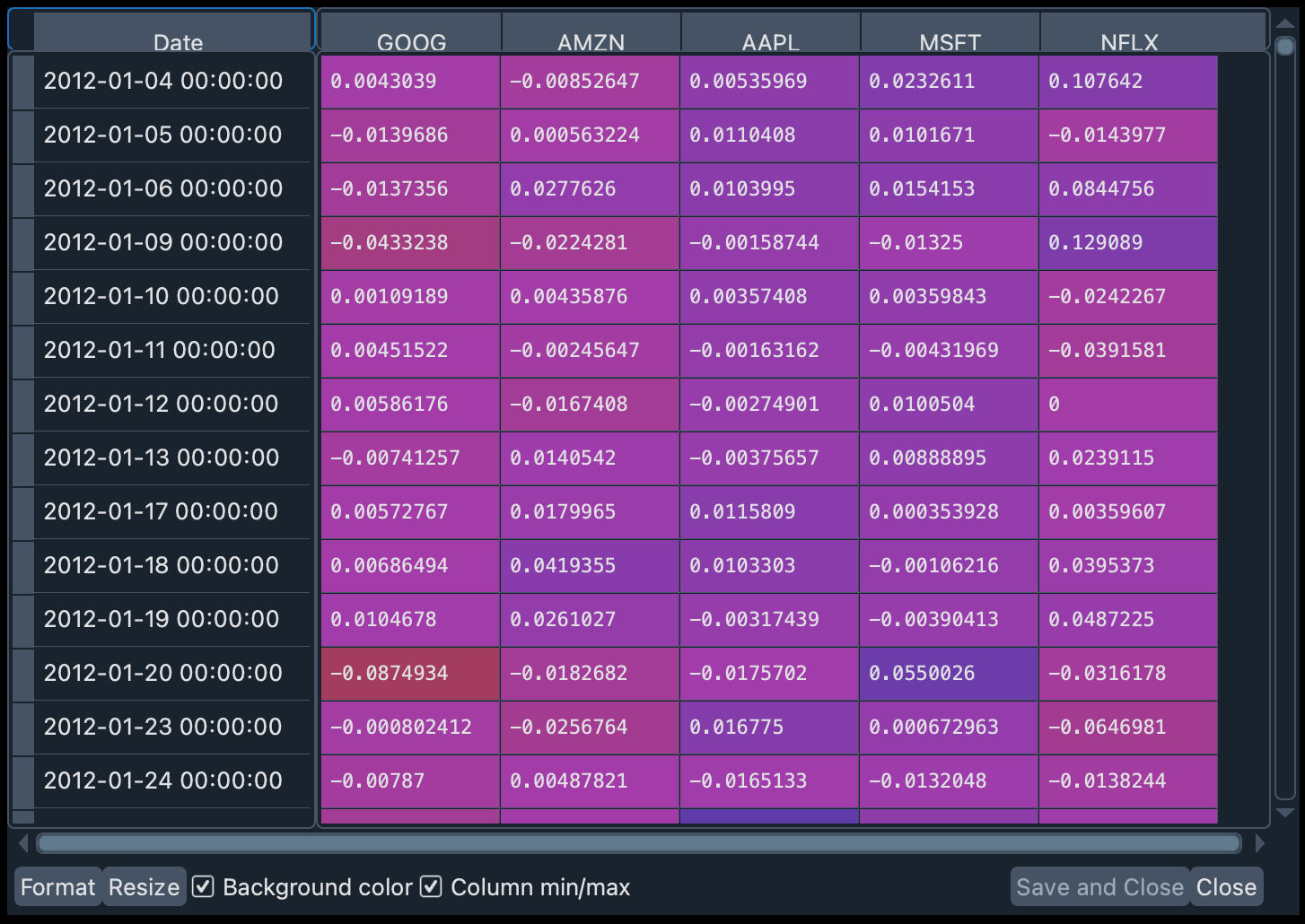
除了每只股票的收益，我们还需要每只股票在投资组合中的具体权重，即投资组合中每家公司有多少股票。在本工作坊中，我们将假设每家公司都有一股股票，因此权重将平均分配。
注意
股票是一种金融证券，代表您拥有一家公司的一部分（无论这部分大小）。而股份是股票的最小面额单位。一股股票由一个或几个股份组成。
此权重将是一个向量（Python 列表），由投资组合中每只股票的相对权重（介于 0 和 1 之间）组成。这些权重的总和必须为 1。由于我们将假设每只股票是一股，因此分配将是相等的：[0.2, 0.2, 0.2, 0.2, 0.2]。
weights_1 = [0.2, 0.2, 0.2, 0.2, 0.2]
有了这些信息，我们就可以计算出这个投资组合的预期收益。计算很简单：它由投资组合权重向量与预期收益向量的点积给出。这个结果必须乘以要计算收益的天数（一年大约有 252 个股票收盘价）。
让我们将这一切放入一个函数中
def portfolio_return(returns, weights):
return np.dot(returns.mean(), weights) * 252
让我们看看这个投资组合持有一年后的预期收益
portfolio_return(rets_1, weights_1)
# 0.2859066023606343
一年内预期收益接近 30%。不错，对吧？但别忘了这枚硬币的另一面：波动性。这个计算有点复杂。首先，计算收益的年化协方差（乘以一年的交易天数）与权重的点积。然后获得权重与前一个结果的点积。最后，提取这个结果的平方根。让我们也将其实现为一个函数。
def portfolio_volatility(returns, weights):
return np.dot(weights, np.dot(returns.cov() * 252, weights)) ** 0.5
让我们看看我们的投资组合在波动性方面表现如何
portfolio_volatility(rets_1, weights_1)
# 0.23704031354688784
如果高收益是可取的，那么高波动性则是不可取的。这个投资组合的风险相对较大。
夏普比率#
夏普比率或指数是衡量投资组合绩效的指标。它将投资组合的收益与其波动性相关联，比较预期/实现收益与预期/实现风险。它的计算方法是实际投资收益与零风险情况下的预期收益之差，再除以投资的波动性。它提供了一个模型，表示每增加一个风险单位所获得的额外收益量。
让我们将此函数化
def portfolio_sharpe(returns, weights):
return portfolio_return(returns, weights) / portfolio_volatility(returns, weights)
让我们将其应用于我们的投资组合。
portfolio_sharpe(rets_1, weights_1)
# 1.2061518063427656
重要
夏普比率最好在上下文中理解：当比较两个或更多投资组合时，夏普比率更高的投资组合在相同风险量下提供更多利润。
我们还可以使用蒙特卡洛模拟来随机化投资组合中每只股票的权重，以便我们可以看到夏普比率的波动范围。通过这种方式，我们可以绘制一些场景，这些场景将共同为我们提供预期收益和预期波动性之间关系的良好洞察。
我们将通过一个函数来完成这项工作，该函数将在蒙特卡洛夏普函数解释部分逐步解释。
def monte_carlo_sharpe(returns, symbols, weights):
sim_weights = np.random.random((1000, len(symbols)))
sim_weights = (sim_weights.T / sim_weights.sum(axis=1)).T
volat_ret = [(portfolio_volatility(returns[symbols], weights), portfolio_return(returns[symbols], weights)) for weights in sim_weights]
volat_ret = np.array(volat_ret)
sharpe_ratio = volat_ret[:, 1] / volat_ret[:, 0]
return volat_ret, sharpe_ratio
警告
您无需在 IPython 控制台中输入以下代码。如果您编写了上述函数就足够了。这只是一个代码展示，用于解释函数内部的内容。
monte_carlo_sharpe 函数解释#
现在让我们分解函数来理解发生了什么。首先，我们创建一个长度为 1,000、宽度为投资组合中股票数量的 numpy 数组。数组的每一行都有随机权重，这些权重总是加起来为 1
sim_weights = np.random.random((1000, len(symbols)))
sim_weights = (sim_weights.T / sim_weights.sum(axis=1)).T
下一节使用列表推导计算新随机权重的波动性和收益。结果列表被转换回 numpy 数组。
volat_ret = [(portfolio_volatility(returns[symbols], weights), portfolio_return(returns[symbols], weights)) for weights in sim_weights]
volat_ret = np.array(volat_ret)
最后，我们通过将索引 1（波动率）除以 numpy 数组的索引 0（收益）来获得夏普比率
sharpe_ratio = volat_ret[:, 1] / volat_ret[:, 0]
使用 monte_carlo_sharpe 函数#
我们使用该函数获取投资组合 1 的模拟收益和波动率（port_1_vr）以及相关的夏普比率（port_1_sr）。
在控制台中输入以下代码。
port_1_vr, port_1_sr = monte_carlo_sharpe(rets_1, SYMBOLS_1, weights_1)
注意
请记住，权重是随机初始化的，因此每次运行此代码都会得到不同的结果。
通过它，我们获得了两个数组，其中包含我们投资组合的 1,000 个模拟案例。但是最好的探索方式是使用绘图。
plt.figure(figsize=(16, 10))
fig = plt.scatter(port_1_vr[:, 0], port_1_vr[:, 1], c=port_1_sr, cmap="cool")
CB = plt.colorbar(fig)
CB.set_label("Sharpe ratio")
plt.xlabel("expected volatility")
plt.ylabel("expected return")
plt.title(" | ".join(SYMBOLS_1))
您应该在绘图窗格中看到类似这样的内容：
收益和波动率之间可以观察到大致线性的关系：波动率越高，收益越高。夏普比率显示出重要的可变性（在绘制的线条“宽度”中很明显）。
这似乎是一个不错的投资组合，因为它表现良好，方差也不大。
最优投资组合权重#
我们可以使用获得的数据来计算每年投资组合的最优权重吗？当然可以。让我们从将前几年定义为变量开始。
start_year, end_year = (2012, 2020)
现在我们将编写一个函数来计算这些最优权重。
def optimal_weights(returns, symbols, actual_weights, start_y, end_y):
bounds = len(symbols) * [(0, 1), ]
constraints = {"type": "eq", "fun": lambda weights: weights.sum() - 1}
opt_weights = {}
for year in range(start_y, end_y):
_rets = returns[symbols].loc[f"{year}-01-01":f"{year}-12-31"]
_opt_w = minimize(lambda weights: -portfolio_sharpe(_rets, weights), actual_weights, bounds=bounds, constraints=constraints)["x"]
opt_weights[year] = _opt_w
return opt_weights
我们大致描述一下这个函数。bounds 表示投资组合中每只股票的最大和最小权重。每只股票的最低权重为 0，最高权重为 1。constraints 是一个函数，确保所有股票的权重之和始终为 1。然后初始化一个循环，将数据按年分割。在变量 _rets 中获取指定年份的收益。在 _opt_w 中，使用 portfolio_shape() 函数计算使夏普比率最大化的权重。这是通过 SciPy 的 minimize() 函数完成的（该函数将 portfolio_shape 函数、投资组合中股票的实际权重以及 bounds 和 constraints 变量作为参数）。注意 portfolio_sharpe 前面的 - 符号吗？那是因为 minimize() 旨在找到函数相对于参数的最小值，但我们对最大值感兴趣，所以我们将 portfolio_sharpe 的结果变为负值。
我们将使用刚刚定义的函数来计算每年的最佳权重，并将结果保存在一个 Pandas DataFrame 中，以便利用变量查看器的显示选项进行查看。
opt_weights_1 = optimal_weights(rets_1, SYMBOLS_1, weights_1, start_year, end_year)
port_1_ow = pd.DataFrame.from_dict(opt_weights_1, orient='index')
port_1_ow.columns = SYMBOLS_1
双击变量查看器中的 port_1_ow 变量。在表格中，您可以通过单击窗格左下角的格式按钮来指定要显示的十进制位数，如下图所示：
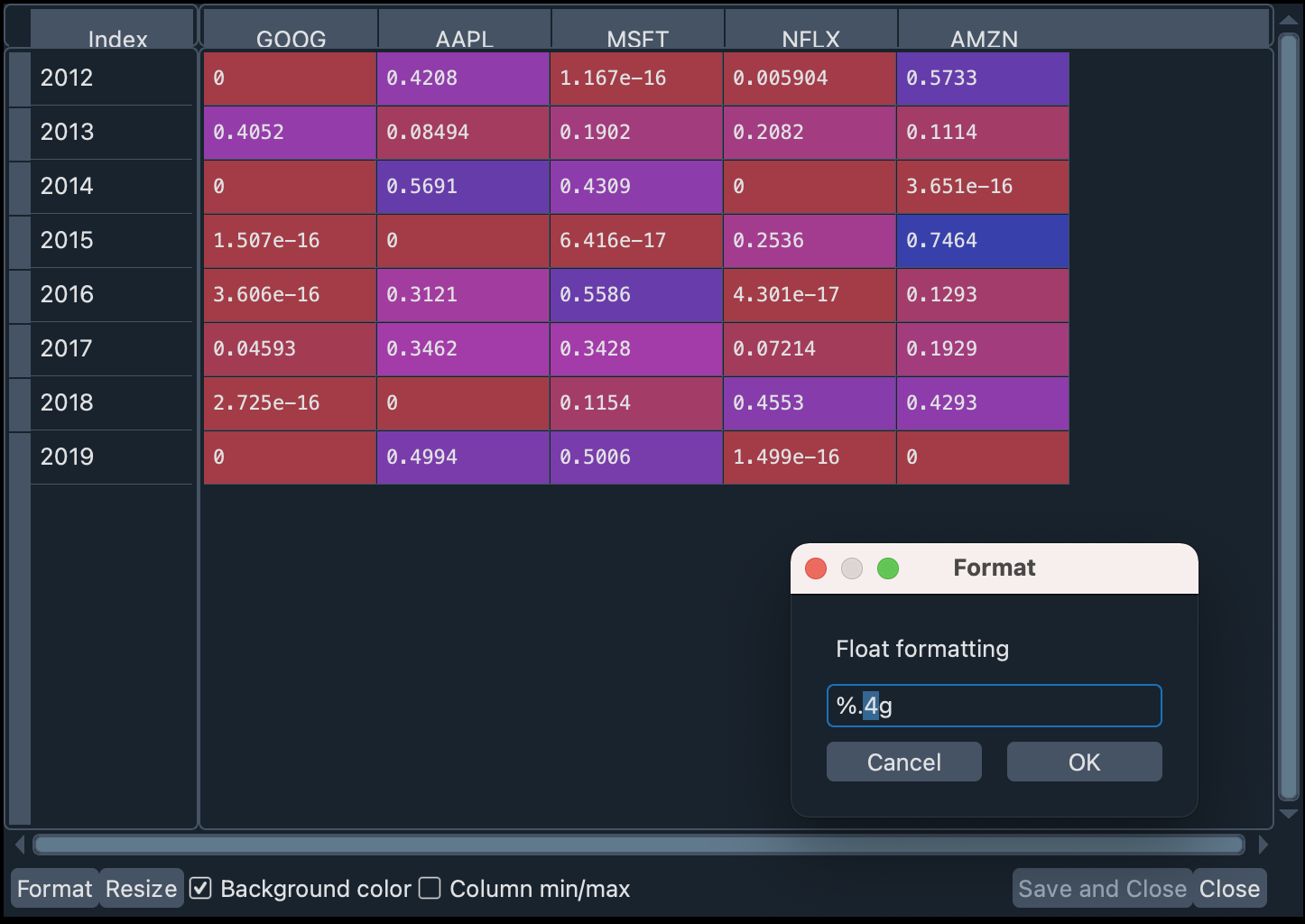
我们将小数位数设置为 4，并取消选中列最小值/最大值复选框，以便更好地体现行值（年份）的对比。
例如，您可以看到 2015 年是投资亚马逊和 Netflix 特别好的一年，而 2014 年是苹果的年份。尽管 Netflix 多年来快速增长，但其高波动性意味着其夏普比率在任何年份都不太显著，尤其是在 2014 年和 2019 年（如我们前面所述）。同样，苹果和微软似乎在收益/波动性比率方面是更安全的押注。
预期收益与实际收益的比较#
最后，我们将使用最优权重来计算预期收益，并将其与实际收益进行比较。
def exp_real_rets(returns, opt_weights, symbols, start_year, end_year):
_rets = {}
for year in range(start_year, end_year):
prev_year = returns[symbols].loc[f"{year}-01-01":f"{year}-12-31"]
current_year = returns[symbols].loc[f"{year + 1}-01-01":f"{year + 1}-12-31"]
expected_pr = portfolio_return(prev_year, opt_weights[year])
realized_pr = portfolio_return(current_year, opt_weights[year])
_rets[year + 1] = [expected_pr, realized_pr]
return _rets
此函数逐年比较实际收益与理论预期收益。这是通过估算以下值完成的：
将上一年股票的最优权重应用于同年数据所获得的收益（
expected_pr）。将上一年股票的最优权重应用于下一年数据所获得的收益（
realized_pr）。
我们将把这个函数应用于投资组合 1 中的数据，并将结果存储在一个 DataFrame 中，以便在变量查看器中查看。
port_1_exp_real = pd.DataFrame.from_dict(exp_real_rets(rets_1, opt_weights_1, SYMBOLS_1, start_year, end_year), orient='index')
port_1_exp_real.columns = ["expected", "realized"]
“expected”列显示如果使用了最优投资组合构成，预测的值。“realized”列则显示使用这些权重实际获得的利润。可以看出，有些年份存在显著差异。让我们在图中看看这一点。
port_1_exp_real.plot(kind="bar", figsize=(16, 10),title="Expected vs. realized Portfolio Returns")
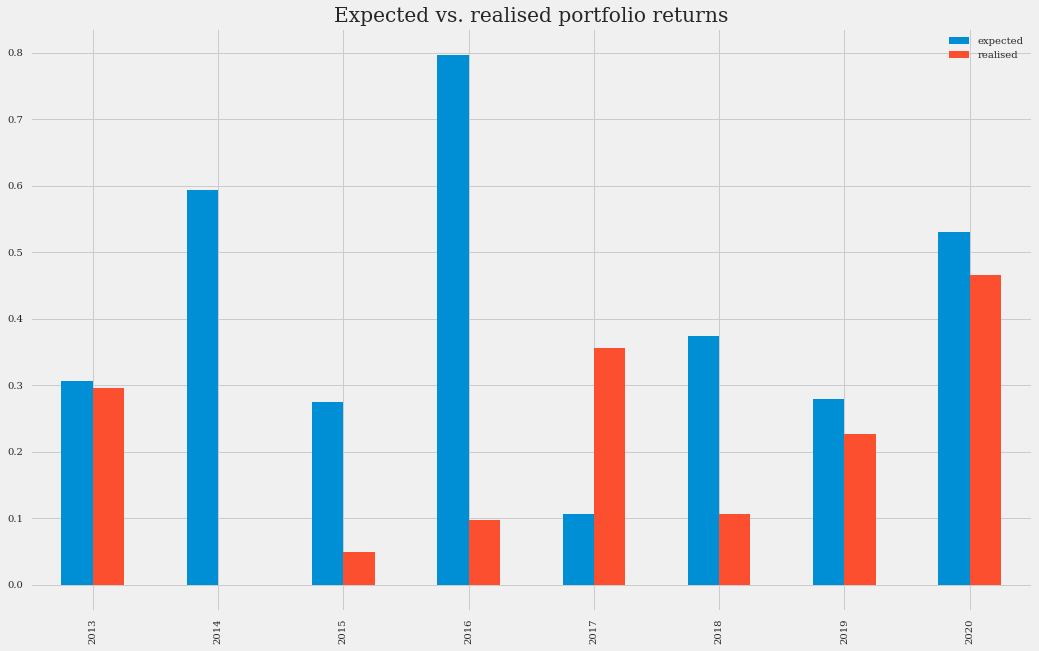
最显著的差异出现在 2014 年和 2016 年。在那些年份，前一年最优投资组合权重（上图中蓝色）是下一年股票表现（红色）的糟糕指标。在 2013 年，我们的模型估计谷歌和 Netflix 是极佳的投资。但到 2014 年，如果我们将年初和年末的价格进行比较，它们的股价并没有增长。2016 年也发生了类似的情况，亚马逊前一年的增长趋势减弱，微软和苹果的股价上涨。
让我们总结这些数字。
port_1_exp_real.mean()
# expected 0.408009
# realized 0.199700
# dtype: float64
我们的最优权重模型给我们带来了大约 40% 的利润，但由于实际市场波动，我们实际获得的利润将接近 20%。还不错，但我们应用于年度计算的均值-方差投资组合模型不是很准确，不是吗？
如果我们计算预期利润和实际利润之间的相关性，这个结果就更不令人鼓舞了。
port_1_exp_real[["expected", "realized"]].corr()
# expected realized
# expected 1.000000 -0.324053
# realized -0.324053 1.000000
正如我们所看到的，相关性是负的，这提醒我们在使用这种建模时应谨慎。
第二个投资组合#
现在我们将把所有前面的代码应用于一个不同性质的投资组合。假设我们现在对制药公司而不是科技公司感兴趣。我们将构建一个包含辉瑞、阿斯利康、强生公司股票的投资组合。
下载数据#
让我们下载数据并进行格式化。
SYMBOLS_2 = ["PFE", "AZN", "JNJ"] # Pfizer, Astra Zeneca, Johnson N Johnson
data_2 = yf.download(" ".join(SYMBOLS_2), start="2012-01-01", end="2021-01-01", group_by="Ticker")
data_2 = data_2.stack(level=1).rename_axis(["Date", "Ticker"]).reset_index(level=1)
close_data_2 = data_2[data_2.Ticker == "Close"].drop("Ticker", inplace=False, axis=1)
注意
如果您不想使用 yfinance API，可以下载包含此投资组合收盘信息的 close_data_2.csv 文件。将此文件复制到您的工作目录。使用以下指令加载数据：>>> close_data_2 = pd.read_csv("close_data_2.csv")。
均值和标准差#
我们将把数据转换为月度格式，并观察均值和标准差。
monthly_data_2 = close_data_2.resample("M").ffill().pct_change()
print("Mean:")
print(monthly_data_2.mean())
print("STD:")
print(monthly_data_2.std())
# Mean:
# AZN 0.008778
# PFE 0.006954
# JNJ 0.009126
# dtype: float64
# STD:
# AZN 0.063068
# PFE 0.053174
# JNJ 0.044063
# dtype: float64
与投资组合 1 类似，所有均值均为正。但其最大值（JNJ）每月仅勉强达到 1%，这比投资组合 1 的增长速度慢。与之前的投资组合相比，其波动性也更小（此处最大偏差为 0.06），这使其成为风险较低的投资。
每日和每月时间线#
让我们用几张图表更好地可视化上述内容。
rets_2 = np.log(close_data_2[SYMBOLS_2] / close_data_2[SYMBOLS_2].shift(1)).dropna()
(close_data_2[SYMBOLS_2] / close_data_2[SYMBOLS_2].iloc[0]).plot(figsize=(16, 10), title="Portfolio 2 daily stock price")
fig = plt.figure()
(monthly_data_2 + 1).cumprod().plot(figsize=(16, 10), title="Portfolio 2 monthly stock price")
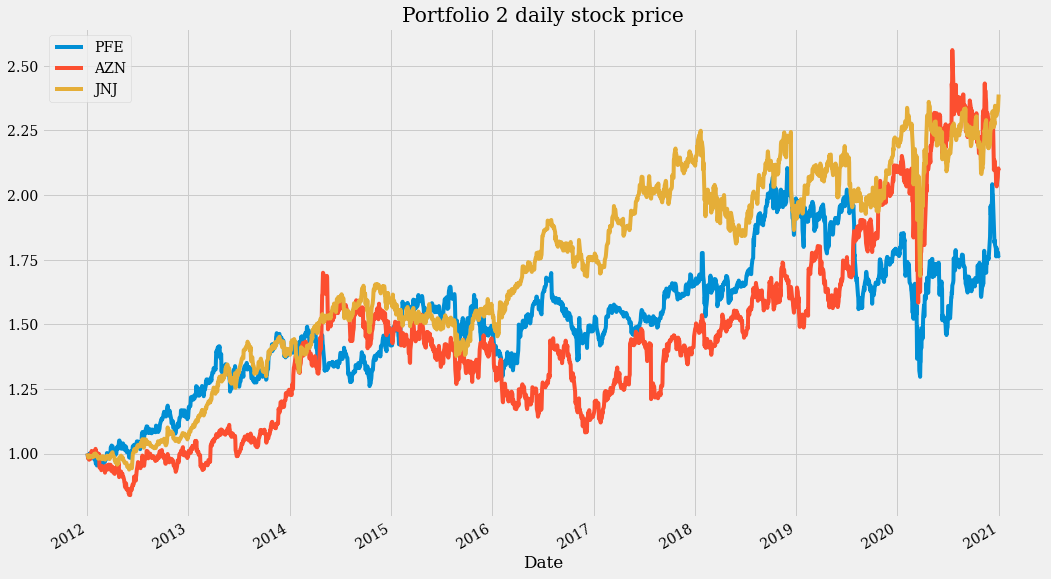
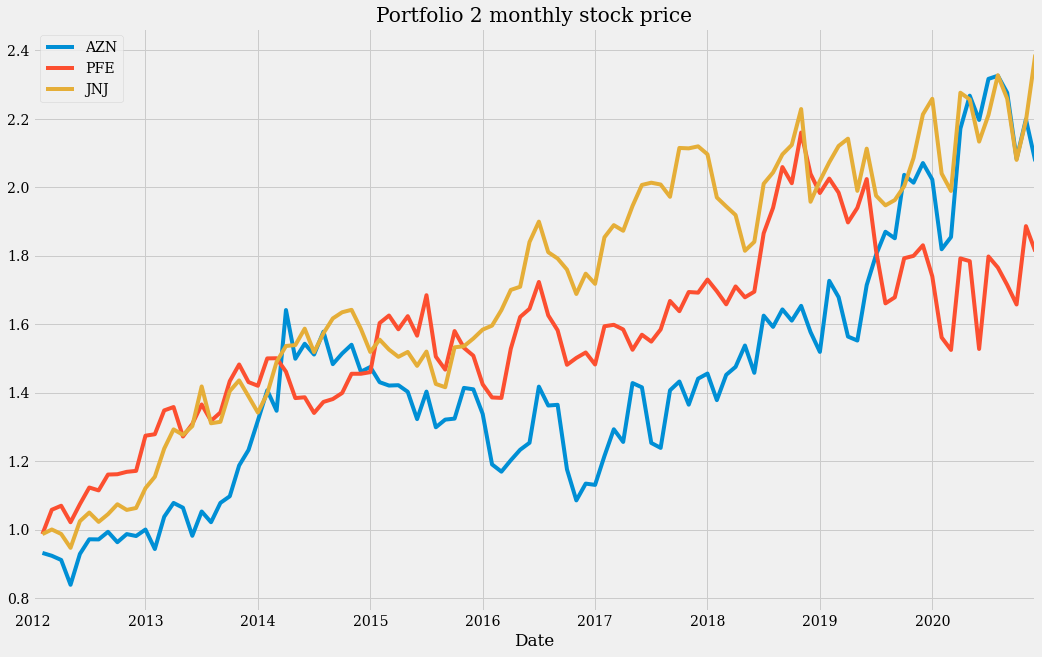
这两张图显示了多年来稳定的增长，但也显示出每年都有很大的波动性。这似乎是一个不错的投资组合，但仅限于作为长期投资。
收益、波动率和夏普比率#
为了证实上一节中所述，我们来计算收益、波动率和夏普比率。
weights_2 = len(close_data_2.columns) * [1 / len(close_data_2.columns)]
print(f"Portfolio 2 returns: {portfolio_return(rets_2, weights_2):.4f}")
print(f"Portfolio 2 volatility: {portfolio_volatility(rets_2, weights_2):.4f}")
print(f"portfolio 2 Sharpe: {portfolio_sharpe(rets_2, weights_2):.4f}")
# Portfolio 2 returns: 0.0809
# Portfolio 2 volatility: 0.1637
# Portfolio 2 Sharpe: 0.4940
该投资组合的收益显著低于前一个投资组合（0.0809 < 0.2859）。其波动率（0.1637 < 0.2370）也较低，但程度较小。这反映在夏普比率也较低（0.4940 < 1.2062）。这意味着，在均值-方差理论方法中，第一个投资组合比第二个投资组合是更好的投资。
如果我们应用蒙特卡洛模拟并用图形将其可视化，则可以清楚地观察到不同的行为
port_2_vr, port_2_sr = monte_carlo_sharpe(rets_2, SYMBOLS_2, weights_2)
plt.figure(figsize=(16, 10))
fig = plt.scatter(port_2_vr[:, 0], port_2_vr[:, 1], c=port_2_sr, cmap="cool")
CB = plt.colorbar(fig)
CB.set_label("Sharpe ratio")
plt.xlabel("expected volatility")
plt.ylabel("expected return")
plt.title(" | ".join(SYMBOLS_2))
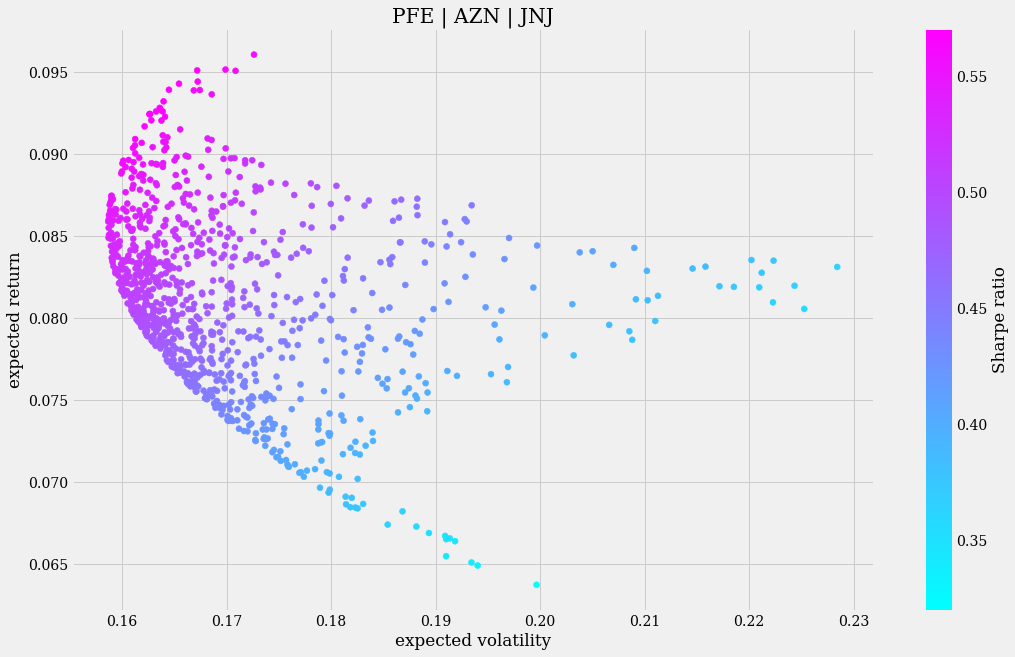
高波动性在大多数情况下并不对应高收益。事实上，在模拟中存在一些场景，其中较高的预期收益与较低的预期波动性相关。
最佳制药股权重#
现在让我们看看使用 optimal_weights 函数，每只股票的最佳权重是多少。
start_year, end_year = (2012, 2020)
opt_weights_2 = optimal_weights(rets_2, SYMBOLS_2, weights_2, start_year, end_year)
port_2_ow = pd.DataFrame.from_dict(opt_weights_2, orient='index')
port_2_ow.columns = SYMBOLS_2
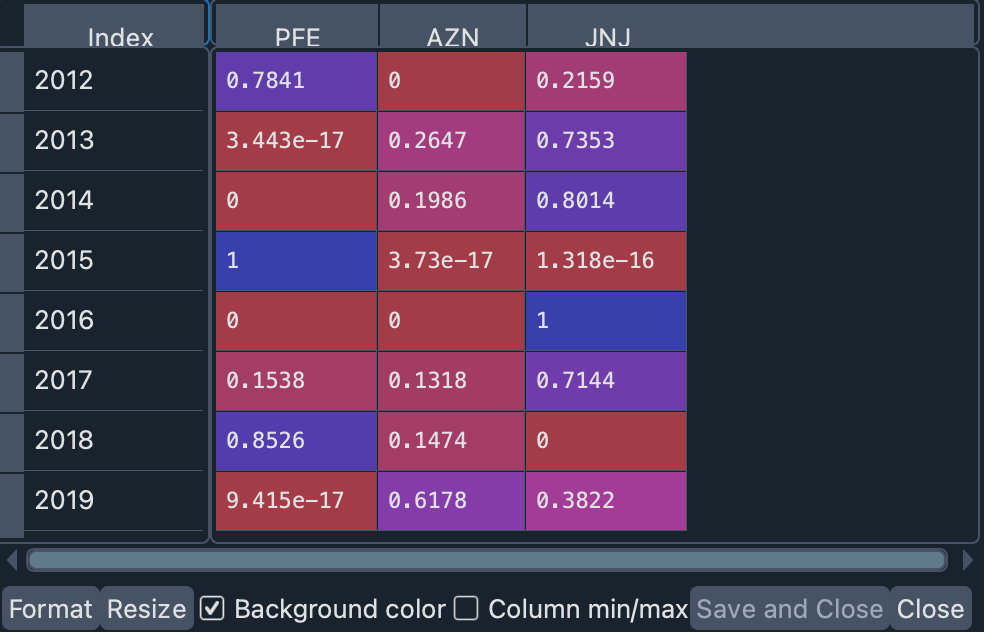
此外，我们可以使用这些最佳权重来绘制该投资组合每年的预期收益和实际收益。
port_2_exp_real = pd.DataFrame.from_dict(exp_real_rets(rets_2, opt_weights_2, SYMBOLS_2, start_year, end_year), orient='index')
port_2_exp_real.columns = ["expected", "realized"]
port_2_exp_real.plot(kind="bar", figsize=(16, 10),title="Expected vs. realized portfolio returns")
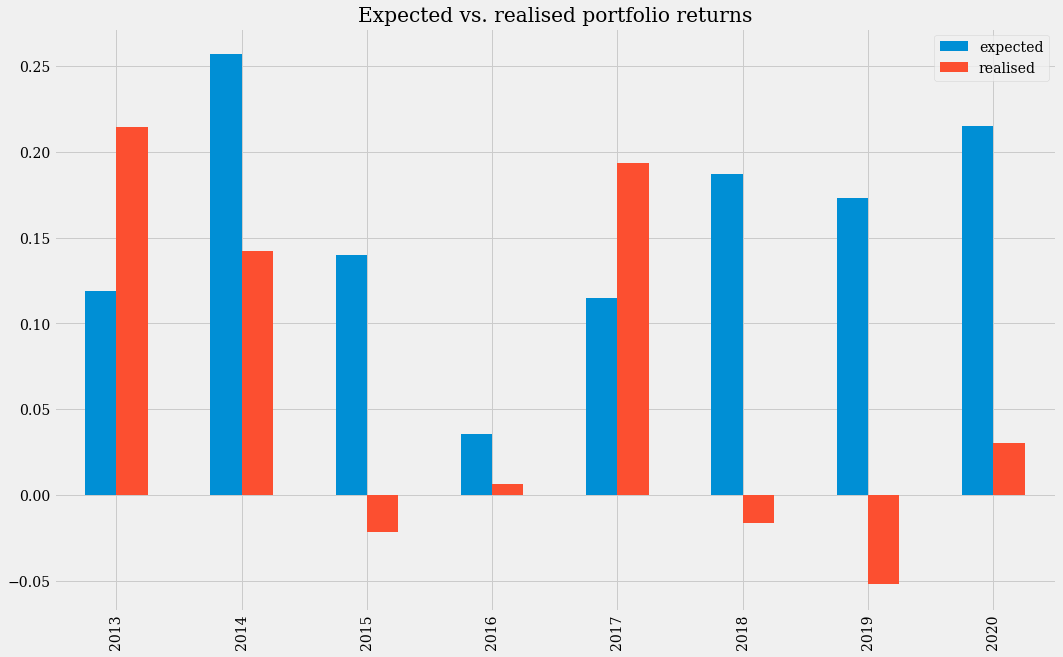
由于此投资组合的高波动性，我们的模型在某些年份未能充分预测预期收益。2013 年和 2017 年的收益会高于预期，但在 2015 年和 2018 年使用该模型会导致亏损。
最后，让我们看看预期均值和实际均值之间的差异，以及数据之间的线性相关性。
print("Expected and realized means:")
print(port_2_exp_real.mean())
print("Expected and realized correlations:")
print(port_2_exp_real[["expected", "realized"]].corr())
# Expected and realized means:
# expected 0.155103
# realized 0.062207
# Expected and realized correlations:
# expected realized
# expected 1.000000 -0.023134
# realized -0.023134 1.000000
正如我们所看到的，具有最优权重的模型预测每年收益接近 15%，但实际收益仅勉强达到 6%。而负相关性表明，与投资组合 1 一样，这些值之间似乎没有任何对应关系。
因此，投资组合 1 的比较结果更有利。但是，如果我们将投资组合 1 与“高风险”投资（如加密货币）进行比较呢？我们将在下面讨论。
第三个投资组合#
下载加密货币数据#
我们的第三个投资组合将由三种加密货币组成：比特币 (BTC)、以太坊 (ETH) 和莱特币 (LTC)。为了访问历史数据，我们将使用一个名为 Historic-Crypto 的库。
重要
如果您想在不使用 Historic-Crypto 库的情况下使用数据，您可以下载数据集“crypto_hist.csv”到您的工作目录，并使用指令 crypto_hist = pd.read_csv("crypto_hist.csv") 将其加载到内存中，然后跳到月度数据部分。
导入库
from Historic_Crypto import Cryptocurrencies
from Historic_Crypto import HistoricalData
我们将使用 Cryptocurrencies 类来获取可用加密货币的列表。
crypto_list = Cryptocurrencies(coin_search="", extended_output=True).find_crypto_pairs()
注意
如果您想了解有关此库使用的更多信息，可以使用 Spyder 帮助面板进行快速查询（在控制台中输入 Cryptocurrencies 并使用 Ctrl-I 或 Cmd-I 显示）。或者您可以在其官方仓库中阅读文档。
变量查看器中出现了一个新变量：crypto_list。它是一个 Pandas DataFrame，对加密货币交易类型有基本描述。例如，我们可以查找哪个代币是以太坊交易（美元计价）的代币。
crypto_list.loc[crypto_list.base_currency == "ETH"]
在这种情况下，我们对 ID 为 171 的符号感兴趣：ETH-USD。
我们可以使用 Historic-Crypto 的 HistoricalData 类下载我们投资组合中以美元计价的加密货币交易历史记录。
# Download and format ETC data:
ETC_HIST = HistoricalData("ETH-USD", 3600 * 24, "2016-01-01-00-00", "2021-01-01-00-00").retrieve_data()
ETC_HIST.rename(columns={"close": "ETC"}, inplace=True)
ETC_HIST.drop(["low", "high", "open", "volume"], axis=1, inplace=True)
# Download and format BTC data:
BTC_HIST = HistoricalData("BTC-USD", 3600 * 24, "2016-01-01-00-00", "2021-01-01-00-00").retrieve_data()
BTC_HIST.rename(columns={"close": "BTC"}, inplace=True)
BTC_HIST.drop(["low", "high", "open", "volume"], axis=1, inplace=True)
# Download and format LTC data:
LTC_HIST = HistoricalData("LTC-USD", 3600 * 24, "2016-01-01-00-00", "2021-01-01-00-00").retrieve_data()
LTC_HIST.rename(columns={"close": "LTC"}, inplace=True)
LTC_HIST.drop(["low", "high", "open", "volume"], axis=1, inplace=True)
让我们合并结果数据帧，将所有数据放在一个表中。
crypto_hist = pd.merge(BTC_HIST, ETC_HIST, on=["time"])
crypto_hist = pd.merge(crypto_hist, LTC_HIST, on=["time"])
在本节中，我们将不介绍程序和代码，而只介绍分析结果。您可以按照前面部分的步骤重新创建这些结果。
注意
使用投资组合 3 的所有部分来检查您对目前所介绍的概念和代码的理解。如果您有任何问题，可以查阅本工作坊附带的代码。但我们鼓励您尽可能地尝试自己解决代码问题。
月度数据#
让我们来看看加密货币价格增长的月度历史。
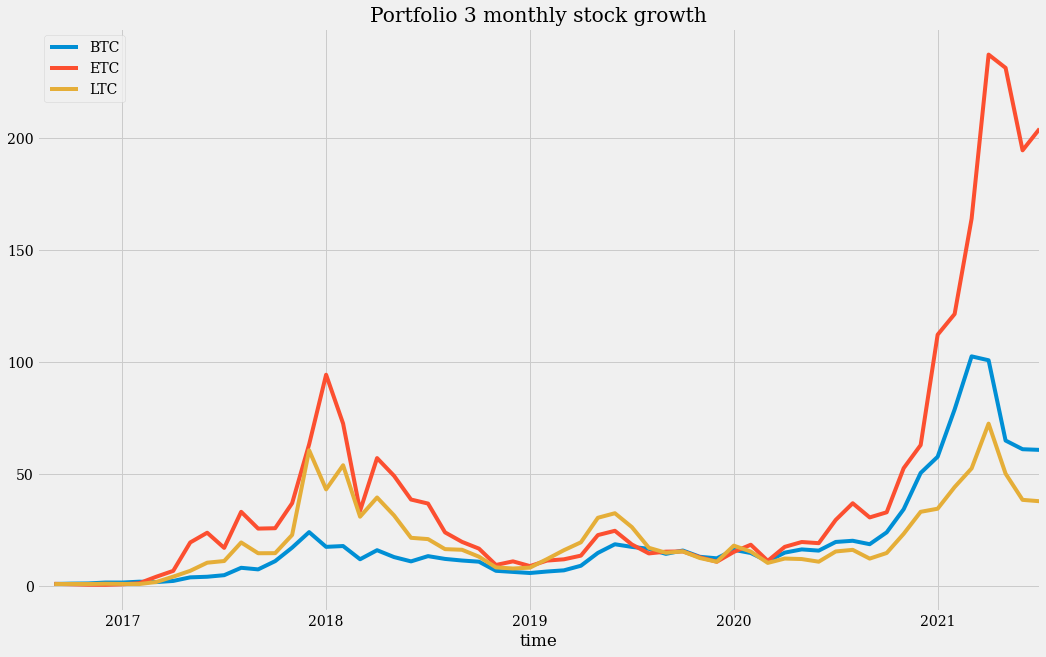
我们可以注意到这里的尺度要大得多。而且以太坊（ETH）的增长比例比其他两种币要显著得多。
收益、波动率和夏普比率#
让我们考虑一下这个投资组合的收益、波动率和夏普比率。
收益率：0.6203
波动率：0.7587
夏普比率：0.8176
这些数字高于投资组合 1 和 2 的数字，除了夏普比率。这是一个波动性非常大的投资组合（实际上是科技公司投资组合的三倍），这使得它最终不如投资组合 1 盈利。收益更高（几乎翻倍），但风险可能不值得。
蒙特卡洛模拟#
蒙特卡洛模拟也显示了风险与收益之间的非线性相关性（如您所见，有时高风险只带来微薄的利润）
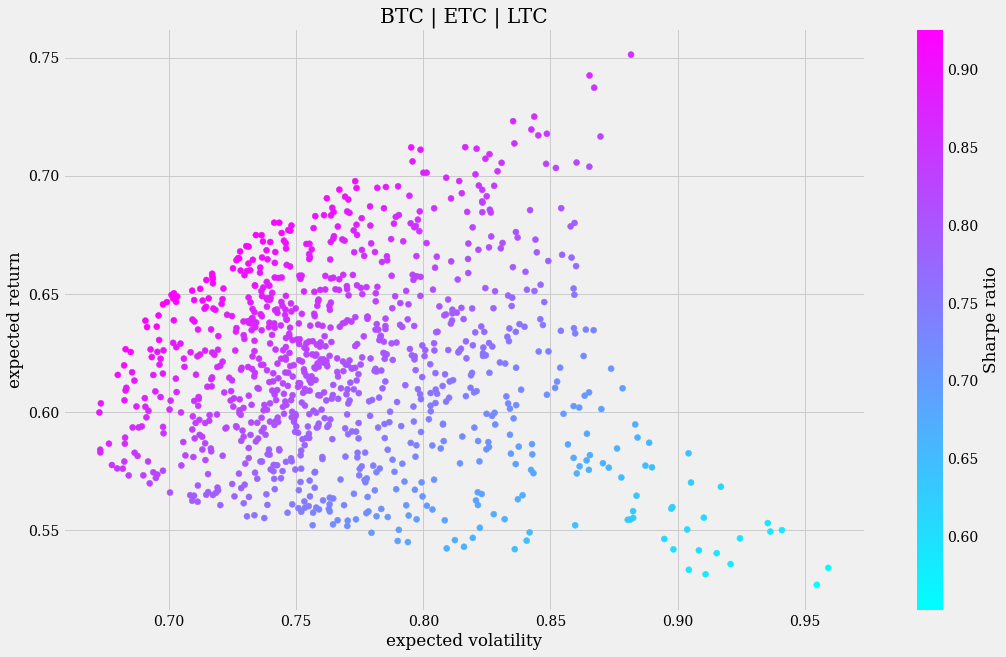
可以看出，有些点（右下角）显示出极高的波动性，但预期收益却非常低。从这个意义上说，投资组合 1 代表着更安全的投资，因为更高的风险始终能被更高的收益所抵消。
最优加密货币权重#
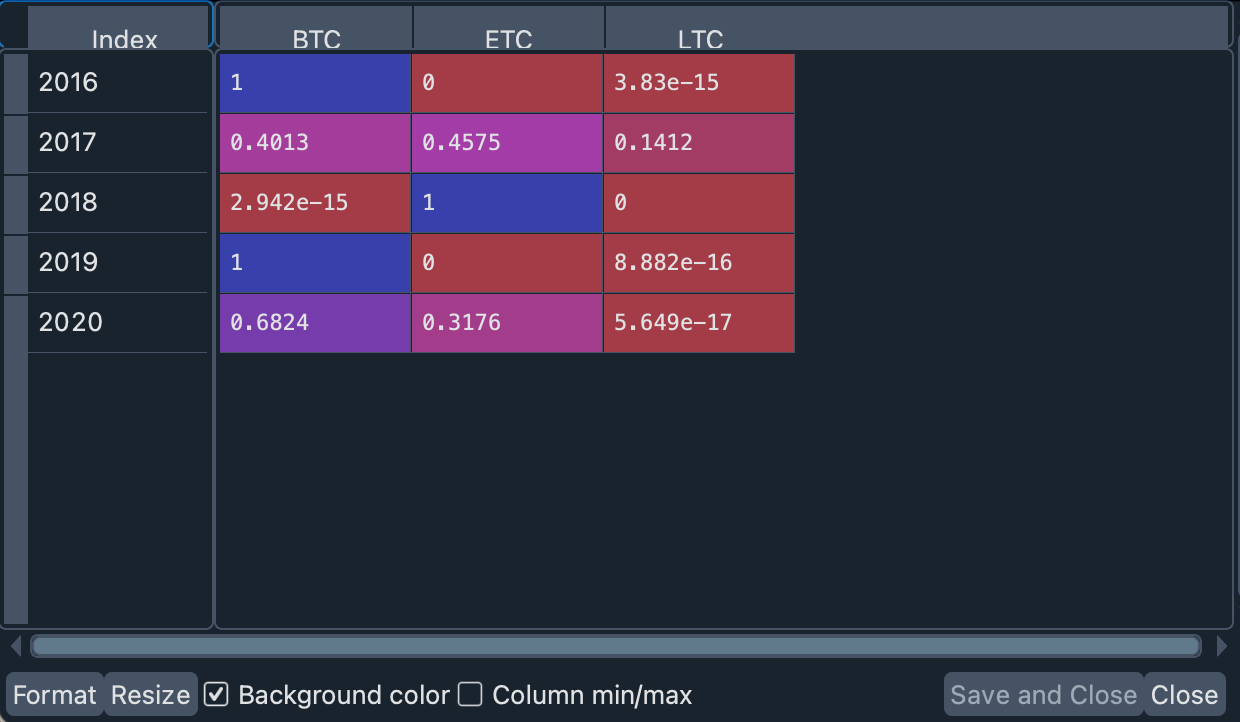
最优投资组合权重，如果每年计算，表明我们的投资组合在某些年份应该非常两极分化：建议在 2016 年和 2019 年初只购买比特币，在 2018 年只购买以太坊。另一方面，从 2017 年和 2020 年开始，我们的权重建议在比特币和以太坊之间进行更平衡的投资。我们的模型不推荐莱特币。
预期收益与实际收益#
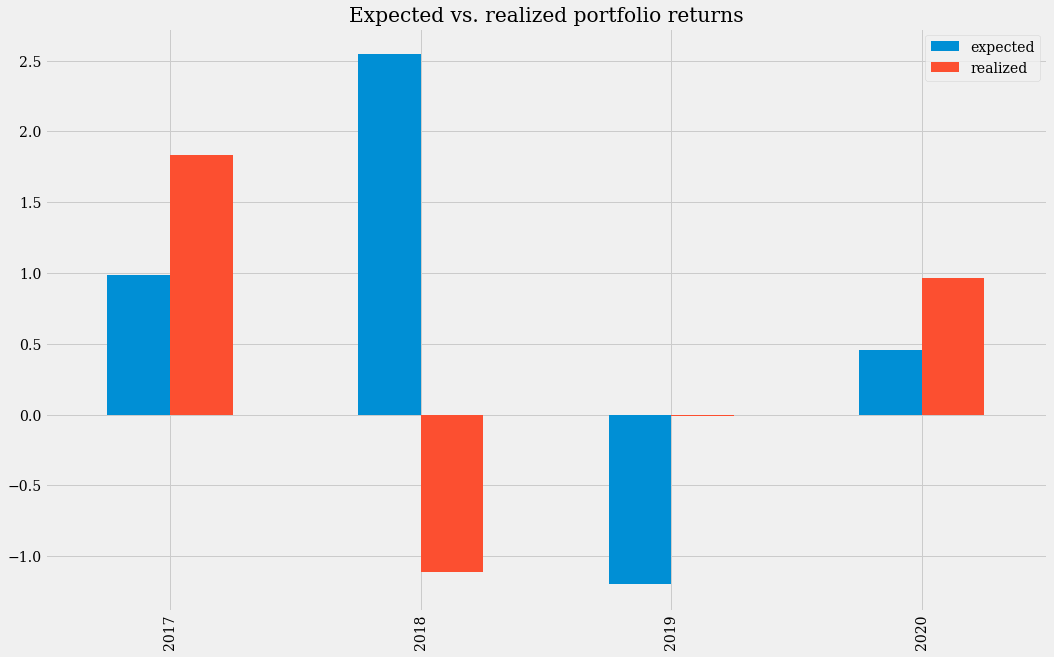
在此图表中，我们可以看到在 2017 年和 2020 年，所获得的收益将超出预期收益（根据我们计算的权重）。在 2019 年，我们的模型预测投资组合会急剧下跌，但实际上该投资组合当年既没有实现年化收益也没有遭受损失。相比之下，在 2018 年，我们的模型会给我们带来巨大损失，因为当年加密货币的价值大幅下跌。
我们投资组合的平均预期收益为 0.6972，高于我们实际获得的 0.4181。长期（从 2016 年至今）投资此投资组合将是一笔非常划算的交易。由于高波动性，短期投资将非常危险。就总利润而言，此投资组合的实际收益是投资组合 1 的两倍多（0.4181 > 0.1997）。
结束语#
均值-方差投资组合 (MVP) 理论是金融分析的众多可用工具之一。近年来，甚至机器学习算法也被用于比任何标准金融理论更准确地预测股票价格行为。
本工作坊中给出的示例并非旨在为您投资提供指导。它只是学习使用 Python 和科学 IDE 进行金融分析的第一步。
在本工作坊中，您已学会如何
设置 Conda 环境。
使用 Spyder 编辑器编写和运行代码。
使用 IPython 控制台编写和测试代码。
使用 API 获取金融数据。
绘制数据图。
在变量查看器中检查对象。
使用绘图窗格浏览绘图。
在 Pandas DataFrame 中操作数据。
构建金融投资组合。
计算投资组合随时间的收益和波动率。
获取投资组合中股票的最优权重。
通过此处学到的技能，您将能够处理更复杂的金融分析主题，例如您将在下一节的参考文献中找到的那些。
感谢您完成本次工作坊！我们希望它对您有所帮助和启发。
如果您对 Spyder 科学计算入门感兴趣，可以访问工作坊使用 Spyder 进行科学计算和可视化。
作业#
如果您想检验所学内容，我们建议您尝试获取第三个投资组合的结果。如果您有任何疑问，可以查阅我们仓库中随本次工作坊提供的代码。
延伸阅读#
用于应用 MVP 的大部分数学知识都出自 Yves Hilpisch 的优秀书籍，我们向您推荐：
Yves Hilpisch, Y. (2020). Artificial Intelligence in Finance. O’Reilly.*
一本陪伴我们几十年、沃伦·巴菲特最喜欢的经典著作：
格雷厄姆，B. (1949). 聪明的投资者. HarperCollins。
另一个使用 Python 进行金融分析的好资源是 James Ma Weiming 的以下书籍：
马伟明，J. (2019). 精通 Python 金融. Packt